



ΖΗΤΗΜΑ 2ο. Αν
 , να βρείτε το
, να βρείτε το  για
για 
ZHTHMA 3o. Να βρείτε το σύνολο των αριθμών
 για τους οποίους αληθεύει η ανισότητα :
για τους οποίους αληθεύει η ανισότητα : , όπου
, όπου 
ZHTHMA 4o. Αν οι αριθμοί
 είναι οι δύο πρώτοι όροι γεωμετρικής προόδου, τότε ο τέταρτος όρος της υπερβαίνει τον τρίτο κατά 18.
είναι οι δύο πρώτοι όροι γεωμετρικής προόδου, τότε ο τέταρτος όρος της υπερβαίνει τον τρίτο κατά 18. Αν δε οι
 και
και 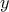 είναι οι δύο πρώτοι όροι αριθμικής προόδου , τότε ο τέταρτος όρος της υπερβαίνει τον δεύτερο κατά 16.
είναι οι δύο πρώτοι όροι αριθμικής προόδου , τότε ο τέταρτος όρος της υπερβαίνει τον δεύτερο κατά 16.Να βρείτε τους αριθμούς
 και
και 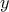 .
.ΖΗΤΗΜΑ 5ο. Να λυθεί το σύστημα :
 και
και 

![\displaystyle{\begin{aligned}\sqrt{\left(\nu+a\right)\left(\nu+b\right)}-\nu &=\frac{\left[\sqrt{\left(\nu+a\right)\left(\nu+b\right)}-\nu\right]\left[\sqrt{\left(\nu+a\right)\left(\nu+b\right)}+\nu\right]}{\left[\sqrt{\left(\nu+a\right)\left(\nu+b\right)}+\nu\right]}\\&=\frac{\left(\nu+a\right)\left(\nu+b\right)-\nu^2}{\left[\sqrt{\left(\nu+a\right)\left(\nu+b\right)}+\nu\right]}\\&=\frac{\left(a+b\right)\nu+ab}{\left[\sqrt{\left(\nu+a\right)\left(\nu+b\right)}+\nu\right]}\\&=\displaystyle{\frac{\left(a+b)+\frac{ab}{\nu}}{\sqrt{\left(1+\frac{a}{\nu}\right)\left(1+\frac{b}{\nu}\right)}+1}}\end{aligned}} \displaystyle{\begin{aligned}\sqrt{\left(\nu+a\right)\left(\nu+b\right)}-\nu &=\frac{\left[\sqrt{\left(\nu+a\right)\left(\nu+b\right)}-\nu\right]\left[\sqrt{\left(\nu+a\right)\left(\nu+b\right)}+\nu\right]}{\left[\sqrt{\left(\nu+a\right)\left(\nu+b\right)}+\nu\right]}\\&=\frac{\left(\nu+a\right)\left(\nu+b\right)-\nu^2}{\left[\sqrt{\left(\nu+a\right)\left(\nu+b\right)}+\nu\right]}\\&=\frac{\left(a+b\right)\nu+ab}{\left[\sqrt{\left(\nu+a\right)\left(\nu+b\right)}+\nu\right]}\\&=\displaystyle{\frac{\left(a+b)+\frac{ab}{\nu}}{\sqrt{\left(1+\frac{a}{\nu}\right)\left(1+\frac{b}{\nu}\right)}+1}}\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/604b09f97bc4cdc290b6ea6d98b99f0c.png)
![\displaystyle{\lim_{n\to \infty}\left[\sqrt{\left(\nu+a\right)\left(\nu+b\right)}-\nu\right]=\lim_{n\to \infty}\frac{\left(a+b)+\frac{ab}{\nu}}{\sqrt{\left(1+\frac{a}{\nu}\right)\left(1+\frac{b}{\nu}\right)}+1}=\frac{a+b}{2}} \displaystyle{\lim_{n\to \infty}\left[\sqrt{\left(\nu+a\right)\left(\nu+b\right)}-\nu\right]=\lim_{n\to \infty}\frac{\left(a+b)+\frac{ab}{\nu}}{\sqrt{\left(1+\frac{a}{\nu}\right)\left(1+\frac{b}{\nu}\right)}+1}=\frac{a+b}{2}}](/forum/ext/geomar/texintegr/latexrender/pictures/dbce1466f34a083552300c7696ca5ad9.png)
![\displaystyle{\begin{aligned} \sqrt{\left(\nu+a\right)\left(\nu+b\right)}-\nu &=\sqrt{\left(\nu+a\right)\left(\nu+b\right)}-\nu-a+a\\&=a+\sqrt{\nu+a}\left[\sqrt{\nu+b}-\sqrt{\nu+a}\right]\\&=a+\sqrt{\nu+a}\left[\frac{b-a}{\sqrt{\nu+b}+\sqrt{\nu+a}}\right]\\&=a+\left(b-a\right)\frac{\sqrt{\nu+a}}{\sqrt{\nu+b}+\sqrt{\nu+a}}\\&=a+\left(b-a\right)\frac{\sqrt{1+\frac{a}{n}}}{\sqrt{1+\frac{b}{n}}+\sqrt{1+\frac{a}{n}}}\end{aligned}} \displaystyle{\begin{aligned} \sqrt{\left(\nu+a\right)\left(\nu+b\right)}-\nu &=\sqrt{\left(\nu+a\right)\left(\nu+b\right)}-\nu-a+a\\&=a+\sqrt{\nu+a}\left[\sqrt{\nu+b}-\sqrt{\nu+a}\right]\\&=a+\sqrt{\nu+a}\left[\frac{b-a}{\sqrt{\nu+b}+\sqrt{\nu+a}}\right]\\&=a+\left(b-a\right)\frac{\sqrt{\nu+a}}{\sqrt{\nu+b}+\sqrt{\nu+a}}\\&=a+\left(b-a\right)\frac{\sqrt{1+\frac{a}{n}}}{\sqrt{1+\frac{b}{n}}+\sqrt{1+\frac{a}{n}}}\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/0dfe47c128fcf7b7f3f6cb35c32ea868.png)
![\displaystyle{\lim_{n\to \infty}\left[\sqrt{\left(\nu+a\right)\left(\nu+b\right)}-\nu\right]=\lim_{n\to \infty}\left[a+\left(b-a\right)\frac{\sqrt{1+\frac{a}{n}}}{\sqrt{1+\frac{b}{n}}+\sqrt{1+\frac{a}{n}}}\right]=a+\frac{b-a}{2}=\frac{a+b}{2}} \displaystyle{\lim_{n\to \infty}\left[\sqrt{\left(\nu+a\right)\left(\nu+b\right)}-\nu\right]=\lim_{n\to \infty}\left[a+\left(b-a\right)\frac{\sqrt{1+\frac{a}{n}}}{\sqrt{1+\frac{b}{n}}+\sqrt{1+\frac{a}{n}}}\right]=a+\frac{b-a}{2}=\frac{a+b}{2}}](/forum/ext/geomar/texintegr/latexrender/pictures/4c0d4be2b937d91193464196b8e76db1.png)
 είναι η Γεωμ. πρόοδος τότε :
είναι η Γεωμ. πρόοδος τότε : 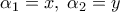 και
και 

 είναι η Αριθμ. πρόοδος τότε :
είναι η Αριθμ. πρόοδος τότε :  και
και 




 τότε
τότε 
 τότε
τότε 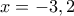
 είναι,
είναι,![\displaystyle{\begin{aligned} f(x)&=x^4-4x^3+6x^2-4x+5\\&=\binom{4}{4}\,x^4\,(-1)^{0}+\binom{4}{3}\,x^3\,(-1)+\binom{4}{2}\,x^2\,(-1)^2+\binom{4}{1}\,x^1\,(-1)^3+1+4\\&=\left[\sum_{k=0}^4 \binom{4}{k}\,x^{k}\,(-1)^{4-k}\right]+4\\&=\left(x-1\right)^4+4\end{aligned}} \displaystyle{\begin{aligned} f(x)&=x^4-4x^3+6x^2-4x+5\\&=\binom{4}{4}\,x^4\,(-1)^{0}+\binom{4}{3}\,x^3\,(-1)+\binom{4}{2}\,x^2\,(-1)^2+\binom{4}{1}\,x^1\,(-1)^3+1+4\\&=\left[\sum_{k=0}^4 \binom{4}{k}\,x^{k}\,(-1)^{4-k}\right]+4\\&=\left(x-1\right)^4+4\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/7efc575be980cbfb0006dbd101f36573.png)

 αφού η συνάρτηση
αφού η συνάρτηση 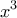 είναι 1-1 στο
είναι 1-1 στο 
 βρίσκουμε
βρίσκουμε  ,
,  που ορίζονται οι ποσότητες
που ορίζονται οι ποσότητες 

 με
με 
 με
με  )
)