 ύψους
ύψους  και πλευράς βάσης
και πλευράς βάσης  . Θεωρούμε τα σημεία
. Θεωρούμε τα σημεία  και
και  μέσα των ακμών
μέσα των ακμών  και
και  αντίστοιχα. Να βρεθεί ο όγκος της πυραμίδας
αντίστοιχα. Να βρεθεί ο όγκος της πυραμίδας  συναρτήσει των
συναρτήσει των 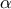 και
και  .
.2. Εαν θεωρήσουμε τέσσερα σημεία
 σε κύκλο, να δειχτεί οτι
σε κύκλο, να δειχτεί οτι  (1), όπου
(1), όπου  το σημείο τομής των
το σημείο τομής των  και
και  , κι αντιστρόφως εαν αληθεύει η σχέση (1), στην περίπτωση που το
, κι αντιστρόφως εαν αληθεύει η σχέση (1), στην περίπτωση που το  είτε βρίσκεται εσωτερικά των
είτε βρίσκεται εσωτερικά των  και
και  είτε βρίσκεται στις προεκτάσεις των
είτε βρίσκεται στις προεκτάσεις των  και
και  , να δειχτεί οτι τα τέσσερα σημεία είναι ομοκυκλικά.
, να δειχτεί οτι τα τέσσερα σημεία είναι ομοκυκλικά.3. Δίνονται δυο εσωτερικά εφαπτόμενοι κύκλοι
 και
και  , των οποίων η διάκεντρος
, των οποίων η διάκεντρος  τέμνει τον εξωτερικό κύκλο
τέμνει τον εξωτερικό κύκλο  στο σημείο
στο σημείο  . Από το
. Από το  φέρνουμε εφαπτομένη στον
φέρνουμε εφαπτομένη στον  . Έστω
. Έστω  η επαφή της με τον κύκλο
η επαφή της με τον κύκλο  . Αυτή προεκτεινόμενη τέμνει τον κύκλο
. Αυτή προεκτεινόμενη τέμνει τον κύκλο  στο
στο 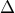 . Εαν
. Εαν  είναι η επαφή των
είναι η επαφή των  και
και  , να δειχτεί οτι η
, να δειχτεί οτι η  είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  .
.4. Δίνεται ορθογώνιο και ισοσκελές τρίγωνο
 (
( ) με κάθετες πλευρές
) με κάθετες πλευρές  . Φέρνουμε τους κύκλους
. Φέρνουμε τους κύκλους  και
και  . Να βρεθεί το εμβαδόν του μικτόγραμμου σχήματος
. Να βρεθεί το εμβαδόν του μικτόγραμμου σχήματος  εαν
εαν 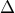 και
και  είναι οι τομές των κύκλων
είναι οι τομές των κύκλων  και
και  με την υποτείνουσα
με την υποτείνουσα  αντίστοιχα.
αντίστοιχα.Υ.Γ. Συμπλήρωση στην εκφώνηση του 2ο θέματος των κόκκινων γραμμάτων έτσι ώστε να ισχύει το αντίστροφο , γιατί σύμφωνα με το Δελτίο του Πάλλα, η πρόταση (1) δεν ισχύει στο αντίστροφο στην περίπτωση που το
 είτε βρίσκεται μεταξύ
είτε βρίσκεται μεταξύ  και
και  και στην προέκταση της
και στην προέκταση της  , είτε βρίσκεται μεταξύ
, είτε βρίσκεται μεταξύ  και
και 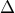 και στην προέκταση της
και στην προέκταση της  .
.
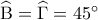 και
και 
 είναι:
είναι: 
 (σχήμα) είναι:
(σχήμα) είναι: 
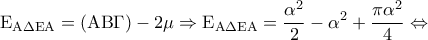

 από το ισοσκελές τρίγωνο
από το ισοσκελές τρίγωνο  .
. ως εντός εναλλάξ (
ως εντός εναλλάξ (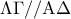 ως κάθετες στην
ως κάθετες στην  )
) , δηλαδή η
, δηλαδή η  είναι διχοτόμος της
είναι διχοτόμος της 
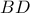 της βάσης
της βάσης  και έτσι συγκρίνουμε τα δύο ζεύγη των τριγωνικών πυραμίδων που προέκυψαν.
και έτσι συγκρίνουμε τα δύο ζεύγη των τριγωνικών πυραμίδων που προέκυψαν.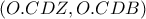 και
και  έχουν αντίστοιχα κοινή την τρίεδρο γωνία της κορυφής των
έχουν αντίστοιχα κοινή την τρίεδρο γωνία της κορυφής των 






 σε σημείο
σε σημείο  του επιπέδου
του επιπέδου  , οπότε
, οπότε  .
.  . Λόγω συμμετρίας, αυτή διέρχεται από τα μέσα
. Λόγω συμμετρίας, αυτή διέρχεται από τα μέσα  των
των  .
.  στο σημείο
στο σημείο  επί της
επί της  . Λόγω συμμετρίας και πάλι το
. Λόγω συμμετρίας και πάλι το  . Από τα όμοια ορθογώνια τρίγωνα
. Από τα όμοια ορθογώνια τρίγωνα 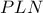 και
και  , και επειδή το
, και επειδή το  , προκύπτουν εύκολα οι
, προκύπτουν εύκολα οι  ,
,  (και
(και  ), οπότε
), οπότε 
 διέρχεται από το σημείο τομής
διέρχεται από το σημείο τομής  των διαγωνίων
των διαγωνίων  και
και  . Παρατηρούμε επίσης ότι η
. Παρατηρούμε επίσης ότι η 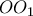 τέμνει και την
τέμνει και την  και
και 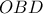 (διάμεσοι), όπου η
(διάμεσοι), όπου η  συγκλίνουν στο
συγκλίνουν στο  και
και 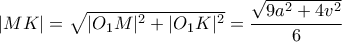 . Από τα όμοια τρίγωνα
. Από τα όμοια τρίγωνα  και
και  προκύπτει τώρα η
προκύπτει τώρα η

 . Και οι δύο μέθοδοι μπορούν να χρησιμοποιηθούν και στην γενικότερη περίπτωση
. Και οι δύο μέθοδοι μπορούν να χρησιμοποιηθούν και στην γενικότερη περίπτωση  , όπου
, όπου  , με αποτέλεσμα
, με αποτέλεσμα  . (Στην δική μου μέθοδο μόνη σημαντική αλλαγή η
. (Στην δική μου μέθοδο μόνη σημαντική αλλαγή η  (με Θεώρημα Μενελάου στο
(με Θεώρημα Μενελάου στο  με διατέμνουσα
με διατέμνουσα  ).)]
).)]