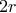 .
.Να βρεθεί πιο έχει το μεγαλύτερο εμβαδόν.
Συντονιστής: xr.tsif
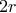 .
.Πολλά πράγματα δεν καταλαβαίνω με την ερώτηση. Πρώτον, τι δουλειά έχει στον φάκελοΦανης Θεοφανιδης έγραψε:Δίνονται άπειρα ορθογώνια τρίγωνα περιμέτρου.
Να βρεθεί πιο έχει το μεγαλύτερο εμβαδόν.
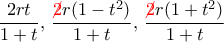 (έκανα μικρή τυπογραφική διόρθωση) όπου
(έκανα μικρή τυπογραφική διόρθωση) όπου  οποιοσδήποτε αριθμός στο (ανοικτό) διάστημα
οποιοσδήποτε αριθμός στο (ανοικτό) διάστημα  . Εύκολα ελέγχουμε, βασιζόμενοι στην ταυτότητα
. Εύκολα ελέγχουμε, βασιζόμενοι στην ταυτότητα  , ότι τα τρίγωνα είναι ορθογώνια και ότι έχουν περίμετρο
, ότι τα τρίγωνα είναι ορθογώνια και ότι έχουν περίμετρο 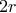 .
. ,
, έχει παράγωγο
έχει παράγωγο  , οπότε είναι γνήσια αύξουσα στο (ανοικτό) διάστημα
, οπότε είναι γνήσια αύξουσα στο (ανοικτό) διάστημα  . Πλην όμως δεν έχει μέγιστη τιμή στο εν λόγω (ανοικτό) διάστημα, που σημαίνει ότι κανένα από τα τρίγωνα δεν έχει το μεγαλύτερο εμβαδόν.
. Πλην όμως δεν έχει μέγιστη τιμή στο εν λόγω (ανοικτό) διάστημα, που σημαίνει ότι κανένα από τα τρίγωνα δεν έχει το μεγαλύτερο εμβαδόν.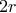 , διαπιστώνω ότι η περίμετρος, έστω
, διαπιστώνω ότι η περίμετρος, έστω  , που μελετήθηκε παραπάνω είναι:
, που μελετήθηκε παραπάνω είναι:


 , άρα σωστή μεν αλλά εκτός θέματος η λύση, τουλάχιστον έτσι νομίζω με τα λίγα μαθηματικά που θυμάμαι και τα επίσης λίγα που μαθαίνω τώρα...
, άρα σωστή μεν αλλά εκτός θέματος η λύση, τουλάχιστον έτσι νομίζω με τα λίγα μαθηματικά που θυμάμαι και τα επίσης λίγα που μαθαίνω τώρα... , μπορούν διαρκώς να μεγαλώνουν και και φυσικά και το μέγιστο εμβαδόν της κάθε περίπτωσης καθώς το
, μπορούν διαρκώς να μεγαλώνουν και και φυσικά και το μέγιστο εμβαδόν της κάθε περίπτωσης καθώς το  πλησιάζει στο
πλησιάζει στο  και ποτέ δεν φτάνει σε αυτό. Αν όμως το διάστημα - και ανεξάρτητα που και πάλι δεν θα έχουμε σταθερή περίμετρο – είναι το
και ποτέ δεν φτάνει σε αυτό. Αν όμως το διάστημα - και ανεξάρτητα που και πάλι δεν θα έχουμε σταθερή περίμετρο – είναι το ![(0,\frac{1}{3}] (0,\frac{1}{3}]](/forum/ext/geomar/texintegr/latexrender/pictures/3ab19af25aff644e4eb0e2e9e59b73f8.png) ;
;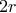 ”, διαισθητικά και με κάποια επιφύλαξη θεωρώ ότι το μεγαλύτερο εμβαδόν το έχει το ισοσκελές.
”, διαισθητικά και με κάποια επιφύλαξη θεωρώ ότι το μεγαλύτερο εμβαδόν το έχει το ισοσκελές.
 .
. 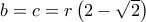 και υποτείνουσα
και υποτείνουσα 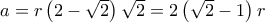
Έχεις δίκιο αλλά πρόκειται για τετριμμένο τυπογραφικό μου σφάλμα. Μπήκαν κάποιαealexiou έγραψε:Θεωρώντας ότι η περίμετρος των άπειρων τριγώνων είναι σταθερή και ίση με, διαπιστώνω ότι η περίμετρος, έστω
, που μελετήθηκε παραπάνω είναι:


 παραπάνω, εκ τυπογραφικής αβλεψίας. Άλλωστε είναι ΠΡΟΦΑΝΕΣ ότι πρόκειται για τυπογραφικό σφάλμα γιατί αμέσως από κάτω γράφω την ταυτότητα
παραπάνω, εκ τυπογραφικής αβλεψίας. Άλλωστε είναι ΠΡΟΦΑΝΕΣ ότι πρόκειται για τυπογραφικό σφάλμα γιατί αμέσως από κάτω γράφω την ταυτότητα  , που δίνει την συνθήκη ορθογωνιότητας (είναι η πασίγνωστες Πυθαγόρειες τριάδες), όπου τα δυάρια δεν (ξανα)μπήκαν. Έκανα την διόρθωση και ζητώ συγνώμη για το, έστω από χιλιόμετρα ορατό, τυπογραφικό μου σφάλμα.
, που δίνει την συνθήκη ορθογωνιότητας (είναι η πασίγνωστες Πυθαγόρειες τριάδες), όπου τα δυάρια δεν (ξανα)μπήκαν. Έκανα την διόρθωση και ζητώ συγνώμη για το, έστω από χιλιόμετρα ορατό, τυπογραφικό μου σφάλμα. Από εδώ φαίνεται ότι μάλλον δεν έγινε κατανοητή η ουσία αυτού που γράφω (πέρα από το τυπογραφικό μου σφάλμα, που είναι όντως σφάλμα). Η ουσία είναι ότι βρήκα άπειρα ορθογώνια τρίγωνα σταθερής περιμέτρου, κανένα από τα οποία δεν έχει μέγιστο εμβαδόν: Το κεντρικό στοιχείο στο αντιπαράδειγμά μου είναι ότι το διάστημα είναι ανοικτό. Αν αλλάξουμε το διάστημα (π.χ. να το κάνουμε κλειστό), τότε πρόκειται ΓΙΑ ΑΛΛΗ οικογένεια ορθογωνίων τριγώνων. Το τι κάνει αυτή η ΑΛΛΗ οικογένεια είναι αδιάφορο. Το ερώτημα είναι αν είναι σωστό το ζητούμενο, και έδειξα ότι δεν είναι είναι.ealexiou έγραψε:Αν όμως το διάστημα - και ανεξάρτητα που και πάλι δεν θα έχουμε σταθερή περίμετρο – είναι το;
Δεν είναι σωστό αυτό ακόμη και αν πάρουμε το διάστημα κλειστό, δηλαδή τοealexiou έγραψε: – είναι το;
Γυρίζοντας στο θέμα που έβαλε ο Φάνης, “άπειρα τρίγωνα περιμέτρου”, διαισθητικά και με κάποια επιφύλαξη θεωρώ ότι το μεγαλύτερο εμβαδόν το έχει το ισοσκελές.
![(0,\frac{1}{3}] (0,\frac{1}{3}]](/forum/ext/geomar/texintegr/latexrender/pictures/3ab19af25aff644e4eb0e2e9e59b73f8.png) . Τώρα έχουμε μεν μέγιστο τρίγωνο, είναι για το
. Τώρα έχουμε μεν μέγιστο τρίγωνο, είναι για το  , πλην όμως το τρίγωνο έχει πλευρές
, πλην όμως το τρίγωνο έχει πλευρές 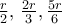 που βέβαια δεν είναι ισοσκελές.
που βέβαια δεν είναι ισοσκελές.
 οι κάθετες πλευρές του τριγώνου που ζητάμε,
οι κάθετες πλευρές του τριγώνου που ζητάμε,  η υποτείνουσα και
η υποτείνουσα και  το εμβαδόν του.
το εμβαδόν του.





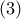
 και
και 
 ,
,  έχουμε πραγματικές λύσεις
έχουμε πραγματικές λύσεις



 και
και  έχουμε ότι
έχουμε ότι 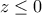 που είναι άτοπο
που είναι άτοπο συμπεραίνουμε ότι η μεγαλύτερη τιμή που μπορεί να
συμπεραίνουμε ότι η μεγαλύτερη τιμή που μπορεί να είναι
είναι 
 και
και 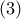 για
για 

Η τιμή αυτή τωνΦανης Θεοφανιδης έγραψε: προκύπτει ότι
 μπορεί να μην είναι από τις επιτρεπτές τιμές που μπορεί να πάρουν τα άπειρα το πλήθος ορθογώνια τρίγωνα της οικογένειάς μας.
μπορεί να μην είναι από τις επιτρεπτές τιμές που μπορεί να πάρουν τα άπειρα το πλήθος ορθογώνια τρίγωνα της οικογένειάς μας.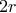 από τα οποία ΚΑΝΕΝΑ από αυτά δεν έχει μέγιστο εμβαδόν.
από τα οποία ΚΑΝΕΝΑ από αυτά δεν έχει μέγιστο εμβαδόν.Τώρα όλα καλά. Όπως ανέφερα, υπάρχουν και καλύτεροι τρόποι απόδειξης του ζητούμενου, οπότε ας δούμε έναν:Φανης Θεοφανιδης έγραψε: διορθώνω την εκφώνηση του θέματος.
 . Άρα, από την
. Άρα, από την 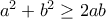 με ισότητα αν και μόνον αν
με ισότητα αν και μόνον αν  , έχουμε
, έχουμε  με ισότητα όταν
με ισότητα όταν  (ισοσκελές). Λύνοντας ως προς
(ισοσκελές). Λύνοντας ως προς  βρίσκουμε αμέσως το μέγιστο εμβαδόν.
βρίσκουμε αμέσως το μέγιστο εμβαδόν.αν και επρόκειτο για ένα οφθαλμοφανές τυπογραφικό (αλλά όχι Μαθηματικό) μου σφάλμα.ealexiou έγραψε: Άρα δεν είναι σταθερή, αφού εξαρτάται από το, άρα σωστή μεν αλλά εκτός θέματος η λύση, τουλάχιστον έτσι νομίζω με τα λίγα μαθηματικά που θυμάμαι
 ή η
ή η 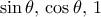 ή όποια άλλη μας βολεύει. Ας μείνουμε στην πρώτη.
ή όποια άλλη μας βολεύει. Ας μείνουμε στην πρώτη.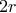 . Κανένα πρόβλημα. Την πολλαπλασιάζουμε επί κατάλληλη σταθερά
. Κανένα πρόβλημα. Την πολλαπλασιάζουμε επί κατάλληλη σταθερά  (που εξαρτάται από τρίγωνο σε τρίγωνο) ώστε να αποκτήσει την περίμετρο που θέλουμε. Τώρα τα τρίγωνα είναι όμοια προς τα αρχικά (για να μην χαλάσουμε την συνθήκη ορθογωνιότητας) και συγκεκριμένα τα
(που εξαρτάται από τρίγωνο σε τρίγωνο) ώστε να αποκτήσει την περίμετρο που θέλουμε. Τώρα τα τρίγωνα είναι όμοια προς τα αρχικά (για να μην χαλάσουμε την συνθήκη ορθογωνιότητας) και συγκεκριμένα τα  .
. . Μα φυσικά
. Μα φυσικά 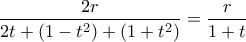
 (αυτή την φορά ήμουν προσεκτικός και δεν έβαλα το παραπανίσιο δυάρι στους δύο αριθμητές. Για κακή μου τύχη μπήκε εκεί επειδή έκανα κοπή/αντιγραφή το πρώτο κλάσμα, και συμπλήρωσα τα υπόλοιπα στοιχεία αλλά ξεχνώντας να σβήσω το παρείσακτο
(αυτή την φορά ήμουν προσεκτικός και δεν έβαλα το παραπανίσιο δυάρι στους δύο αριθμητές. Για κακή μου τύχη μπήκε εκεί επειδή έκανα κοπή/αντιγραφή το πρώτο κλάσμα, και συμπλήρωσα τα υπόλοιπα στοιχεία αλλά ξεχνώντας να σβήσω το παρείσακτο  .)
.)  . Μένει να επιλέξουμε διάστημα μεταβολής παραμέτρου
. Μένει να επιλέξουμε διάστημα μεταβολής παραμέτρου  , κάποιο διάστημα που η συνάρτηση του εμβαδού δεν έχει μέγιστο. Ένας τρόπος (ο ευκολότερος) είναι να εντοπίσουμε ένα διάστημα όπου η συνάρτηση είναι αύξουσα, αλλά να κόψουμε το δεξί άκρο (όπου θα λάμβανε το μέγιστο). Έτσι δεν λαμβάνει μέγιστο.
, κάποιο διάστημα που η συνάρτηση του εμβαδού δεν έχει μέγιστο. Ένας τρόπος (ο ευκολότερος) είναι να εντοπίσουμε ένα διάστημα όπου η συνάρτηση είναι αύξουσα, αλλά να κόψουμε το δεξί άκρο (όπου θα λάμβανε το μέγιστο). Έτσι δεν λαμβάνει μέγιστο. Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες