Α.Αποστόλου έγραψε:Αν αλλάζει η μονοτονία της συνάρτησης σε εσωτερικό σημείο του διαστήματος,
πρέπει να έχουμε τοπικό ακρότατο . Αυτό το καλύψαμε.
Άρα είναι μονότονη.
Είναι γνησίως μονότονη, το καλύψαμε και αυτό με το Rolle (με μια πιο "ελεύθερη" διατύπωση, ώστε να μην είναι πλήρως μασημένη τροφή)
Εφόσονrek2 έγραψε: Γιατί;; Πως προκύπτει το " γνησίως αύξουσα";;με
Μάλιστα, θεωρώ ότι ήδη γράφω πολλά, αφού απο το σχόλιο στην σελίδα 261 τα μοναδικά κρίσιμα σημεία της δοσμένης
είναι τα άκρα του διαστήματος. Απο το σχόλιο στην σελίδα 264 δεν χρειάζεται να ξαναναφέρω το θεώρημα μέγιστης και ελάχιστης τιμής.
Να ζητάμε απόδειξη ότι παραγωγίσιμη συνάρτηση χωρίς εσωτερικά κρίσιμα σημεία -για την οποία προκύπτει εύκολα ότι είναι "1-1"- πως είναι γνησίως μονότονη,
μάλλον είναι πλεονασμός.
Η παράγωγος διατηρεί σταθερό πρόσημο (της δοσμένης συνάρτησης πάντα)
Έχουμε απο Θ.Μ.Τ. ότι υπάρχειτέτοιο ώστε:
Έστω ότι υπάρχειμε
τότε ξανά απο Θ.Μ.Τ. ότι υπάρχειτέτοιο ώστε
Τότε για κάποιοστο
(δεν έχει σημασία η διάταξη) η παράγωγος δεν διατηρεί πρόσημο.
απο το θεώρημα σελ.262 σε κάποιοη συνάρτηση παρουσιάζει τοπικό ακρότατο.
Καθώς είναι παραγωγίσιμη παντού, για αυτό τοθα μηδενίστεί η παράγωγος, άτοπο.
Σε καμία περίπτωση δεν είναι προφανή τα παραπάνω!
Μάλλον δημιουργούν περισσότερη σύγχυση!
Μια απόδειξη της μονοτονίας μέσω ακροτάτων υπάρχει εδώ: viewtopic.php?f=61&t=51621



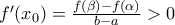


 η δοθείσα σχέση γράφεται
η δοθείσα σχέση γράφεται  (1).
(1).  η
η  είναι γνήσια αύξουσα στο
είναι γνήσια αύξουσα στο  και επειδή είναι συνεχής
και επειδή είναι συνεχής 
 άρα το σύνολο τιμών της
άρα το σύνολο τιμών της  είναι το σύνολο τιμών της
είναι το σύνολο τιμών της  άρα το
άρα το  , για την οποία ισχύουν:
, για την οποία ισχύουν:![\displaystyle \bullet f\left ( e^{f'(x)} \right )+ln\left [ xf'(x) \right ]=f\left ( e^{\frac{1}{x}} \right ) \displaystyle \bullet f\left ( e^{f'(x)} \right )+ln\left [ xf'(x) \right ]=f\left ( e^{\frac{1}{x}} \right )](/forum/ext/geomar/texintegr/latexrender/pictures/7b1c7ade30f5a13e3d193965c4f03f28.png) , για κάθε
, για κάθε  .
.
 , για κάθε
, για κάθε  , ώστε το εμβαδόν του χωρίου που περικλείεται από τη
, ώστε το εμβαδόν του χωρίου που περικλείεται από τη  και τις ευθείες
και τις ευθείες  και
και  , να είναι ίσο με
, να είναι ίσο με  τετραγωνικές μονάδες.
τετραγωνικές μονάδες. υπάρχουν
υπάρχουν  τέτοια ώστε
τέτοια ώστε ![\displaystyle f\left [ \left ( \frac{\alpha +\beta }{2} \right )^{y+z} \right ]=y\cdot f(\alpha )+z\cdot f(\beta ) \displaystyle f\left [ \left ( \frac{\alpha +\beta }{2} \right )^{y+z} \right ]=y\cdot f(\alpha )+z\cdot f(\beta )](/forum/ext/geomar/texintegr/latexrender/pictures/637991888ff1fa5ad5af258f85f40a1a.png) .
. , με
, με  , και η εφαπτομένη της
, και η εφαπτομένη της  , με
, με  , στο σημείο
, στο σημείο  ταυτίζονται, τότε να αποδείξετε ότι ο αριθμός
ταυτίζονται, τότε να αποδείξετε ότι ο αριθμός  είναι ρίζα της εξίσωσης
είναι ρίζα της εξίσωσης  .
.
![f\left( {{e}^{{f}'(x)}} \right)+ln\left[ x{f}'(x) \right]=f\left( {{e}^{\frac{1}{x}}} \right) f\left( {{e}^{{f}'(x)}} \right)+ln\left[ x{f}'(x) \right]=f\left( {{e}^{\frac{1}{x}}} \right)](/forum/ext/geomar/texintegr/latexrender/pictures/e749b854c553b2d494cfe08cbb4d6357.png) (1)για κάθε
(1)για κάθε  για κάθε
για κάθε  για κάθε
για κάθε  στο
στο 

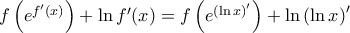 (2)
(2) επειδή είναι παραγωγίσιμη με
επειδή είναι παραγωγίσιμη με 
 (3)
(3) αν
αν  τότε
τότε  και επομένως
και επομένως  αφού
αφού ![x{{e}^{x}}\ge 0,\,\,\,x\in [0,\,\,f(1)] x{{e}^{x}}\ge 0,\,\,\,x\in [0,\,\,f(1)]](/forum/ext/geomar/texintegr/latexrender/pictures/1c554d365be3c1348aaa6a222723c881.png) που είναι άτοπο, ή
που είναι άτοπο, ή 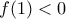 και επομένως
και επομένως 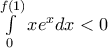 αφού
αφού ![x{{e}^{x}}\le 0,\,\,\,x\in [f(1),\,\,0] x{{e}^{x}}\le 0,\,\,\,x\in [f(1),\,\,0]](/forum/ext/geomar/texintegr/latexrender/pictures/64bce51117738960708c92177226e883.png) που είναι άτοπο, άρα αναγκαία
που είναι άτοπο, άρα αναγκαία 
 , οπότε
, οπότε 
 (4)
(4) ![\int\limits_{3}^{9}{\ln xdx}=\left[ x\ln x-x \right]_{3}^{9}=9\ln 9-9-3\ln 3+3=15\ln 3-6 \int\limits_{3}^{9}{\ln xdx}=\left[ x\ln x-x \right]_{3}^{9}=9\ln 9-9-3\ln 3+3=15\ln 3-6](/forum/ext/geomar/texintegr/latexrender/pictures/57af95eea8b9cbdcd2a1aff4c95d0c89.png)
 και τώρα η συνάρτηση
και τώρα η συνάρτηση ![g(x)=\int\limits_{x}^{{{x}^{2}}}{\ln tdt=\left[ t\ln t-t \right]_{x}^{{{x}^{2}}}={{x}^{2}}\ln {{x}^{2}}-{{x}^{2}}-xlnx+x\Leftrightarrow } g(x)=\int\limits_{x}^{{{x}^{2}}}{\ln tdt=\left[ t\ln t-t \right]_{x}^{{{x}^{2}}}={{x}^{2}}\ln {{x}^{2}}-{{x}^{2}}-xlnx+x\Leftrightarrow }](/forum/ext/geomar/texintegr/latexrender/pictures/f6e6bd288f4bbc274ca261a2b69a8458.png)
 είναι παραγωγίσιμη με
είναι παραγωγίσιμη με  άρα είναι γνήσια αύξουσα
άρα είναι γνήσια αύξουσα  επομένως από (4)
επομένως από (4) 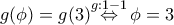

![\displaystyle \left [ \alpha ,\frac{\alpha +\beta }{2} \right ] \displaystyle \left [ \alpha ,\frac{\alpha +\beta }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/2e8eda776523602964360cc095cc68e0.png) και
και ![\displaystyle \left [\frac{\alpha +\beta }{2},\beta \right ] \displaystyle \left [\frac{\alpha +\beta }{2},\beta \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/1e74d471b745d289f45954879940f8c9.png) αντίστοιχα, οπότε υπάρχει:
αντίστοιχα, οπότε υπάρχει: ώστε να ισχύει
ώστε να ισχύει 
 , σχέση
, σχέση  .
. τέτοιο ώστε να ισχύει:
τέτοιο ώστε να ισχύει:
 , σχέση
, σχέση  .
. έπεται το ζητούμενο.
έπεται το ζητούμενο.
 , με
, με  .
. , για κάθε
, για κάθε  .
. , για κάθε
, για κάθε  και τις ευθείες
και τις ευθείες  και
και  .
. , ώστε τα σημεία
, ώστε τα σημεία  ,
,  και
και  , να είναι συνευθειακά.
, να είναι συνευθειακά. και
και  και
και  άρα η
άρα η  και
και 
![(-\infty ,\,\,\alpha -1] (-\infty ,\,\,\alpha -1]](/forum/ext/geomar/texintegr/latexrender/pictures/071961adddf9131decab98ecad2e308b.png) επομένως η
επομένως η  το
το  άρα ισχύει ότι
άρα ισχύει ότι 
 για
για  (1)
(1)![{{\Delta }_{1}}=(-\infty ,\,\,\alpha -1] {{\Delta }_{1}}=(-\infty ,\,\,\alpha -1]](/forum/ext/geomar/texintegr/latexrender/pictures/b9b99ebc9ad9716fef781c1f1c7440a3.png) οπότε
οπότε 

 η
η 
 δηλαδή
δηλαδή  και τότε για τις τιμές από (1) που
και τότε για τις τιμές από (1) που έχει μοναδική λύση στο
έχει μοναδική λύση στο 
 έχουμε
έχουμε 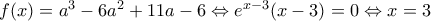
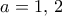 μοναδικές λύσεις τις
μοναδικές λύσεις τις  αντίστοιχα.
αντίστοιχα. είναι
είναι 
 η εξίσωση είναι αδύνατη
η εξίσωση είναι αδύνατη  η εξίσωση θα έχει μοναδική ρίζα την
η εξίσωση θα έχει μοναδική ρίζα την  η εξίσωση δύο ρίζες μία στο
η εξίσωση δύο ρίζες μία στο 

 και επειδή
και επειδή  είναι
είναι  άρα
άρα ![E=-\int\limits_{-a}^{a}{{{e}^{x-a}}(x-a)dx}=-\left[ {{e}^{x-a}}(x-a) \right]_{-a}^{a}+\int\limits_{-a}^{a}{{{e}^{x-a}}dx}= E=-\int\limits_{-a}^{a}{{{e}^{x-a}}(x-a)dx}=-\left[ {{e}^{x-a}}(x-a) \right]_{-a}^{a}+\int\limits_{-a}^{a}{{{e}^{x-a}}dx}=](/forum/ext/geomar/texintegr/latexrender/pictures/acee285b77ce06afcd83f8ae9fc1e616.png)
![=2a{{e}^{-2a}}+\left[ {{e}^{x-a}} \right]_{-a}^{a}=2a{{e}^{-2a}}+1-{{e}^{-2a}} =2a{{e}^{-2a}}+\left[ {{e}^{x-a}} \right]_{-a}^{a}=2a{{e}^{-2a}}+1-{{e}^{-2a}}](/forum/ext/geomar/texintegr/latexrender/pictures/69be73b2ac308cb95facc06426d7fd94.png)

 και επειδή
και επειδή 
 άρα
άρα ![E=\int\limits_{a}^{-a}{{{e}^{x-a}}(x-a)dx}=\left[ {{e}^{x-a}}(x-a) \right]_{a}^{-a}-\int\limits_{a}^{-a}{{{e}^{x-a}}dx}= E=\int\limits_{a}^{-a}{{{e}^{x-a}}(x-a)dx}=\left[ {{e}^{x-a}}(x-a) \right]_{a}^{-a}-\int\limits_{a}^{-a}{{{e}^{x-a}}dx}=](/forum/ext/geomar/texintegr/latexrender/pictures/2d4158fd692f57e6d5a282185f7e649a.png)
![=-2a{{e}^{-2a}}-\left[ {{e}^{x-a}} \right]_{a}^{-a}=-2a{{e}^{-2a}}+1-{{e}^{-2a}} =-2a{{e}^{-2a}}-\left[ {{e}^{x-a}} \right]_{a}^{-a}=-2a{{e}^{-2a}}+1-{{e}^{-2a}}](/forum/ext/geomar/texintegr/latexrender/pictures/05b884eb59e218c1f7ed3882d8563f87.png)
 με τις ιδιότητες :
με τις ιδιότητες : , για κάθε
, για κάθε  και
και  .
. .
. ,
,  .
. .
.![f''(x)=-2x[f'(x)]^{2} f''(x)=-2x[f'(x)]^{2}](/forum/ext/geomar/texintegr/latexrender/pictures/48c9c91e0013d1002203b8a4be607762.png) , για κάθε
, για κάθε  .
. , με
, με ![h(x)= \int_{1}^{x} [f'(t)]^{2} dt h(x)= \int_{1}^{x} [f'(t)]^{2} dt](/forum/ext/geomar/texintegr/latexrender/pictures/7b0979ffebbc4307d138c3da16da77de.png) και τις ευθείες με εξισώσεις
και τις ευθείες με εξισώσεις  ,
,  και
και  .
.
 επειδη έχει παράγωγο θετική θα είναι γν.αύξουσα.
επειδη έχει παράγωγο θετική θα είναι γν.αύξουσα. και μελετώντας τα όρια
και μελετώντας τα όρια  αρα για την \
αρα για την \ ετσι οι ασύμπτωτες είναι
ετσι οι ασύμπτωτες είναι 




![\displaystyle f:\left [ 0,\frac{\pi }{2} \right ]\rightarrow \mathbb{R} \displaystyle f:\left [ 0,\frac{\pi }{2} \right ]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/c596ed90e9745854316b817a9fb28870.png) , με:
, με:

 με
με  είναι σταθερή και να βρείτε το τύπο της
είναι σταθερή και να βρείτε το τύπο της 
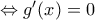
 .
. , θα είναι και
, θα είναι και 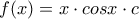 .
. .
.

 και επειδή
και επειδή  θα είναι και συνεχής στο
θα είναι και συνεχής στο 
 , έχουμε
, έχουμε  .
. , για κάθε
, για κάθε  .
. . Δείξτε ότι τα σημεία στα οποία η
. Δείξτε ότι τα σημεία στα οποία η  είναι κορυφές παραλληλογράμμου καθώς επίσης και ότι οι εφαπτομένες της
είναι κορυφές παραλληλογράμμου καθώς επίσης και ότι οι εφαπτομένες της  στα σημεία που παρουσιάζει καμπή τέμνονται σε σταθερή υπερβολή.
στα σημεία που παρουσιάζει καμπή τέμνονται σε σταθερή υπερβολή. είναι το
είναι το  , οπότε
, οπότε και τοπικό μέγιστο στο σημείο
και τοπικό μέγιστο στο σημείο  .
. . Πάλι ... κατά τα γνωστά συμπεραίνουμε ότι η
. Πάλι ... κατά τα γνωστά συμπεραίνουμε ότι η  και
και  .
. σημείο καμπής , αλλά δεν μας ενδιαφέρει.
σημείο καμπής , αλλά δεν μας ενδιαφέρει.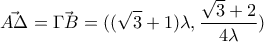 , συνεπώς το τετράπλευρο με κορυφές τα
, συνεπώς το τετράπλευρο με κορυφές τα και
και  είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο. ισχύει :
ισχύει :  και
και  από όπου με πολλαπλασιασμό κατά μέλη προκύπτει
από όπου με πολλαπλασιασμό κατά μέλη προκύπτει  .
.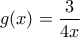 .
. με
με 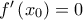 και
και  .
. , για κάθε
, για κάθε  .
. , για κάθε
, για κάθε  .
. είναι συνεχής στο διάστημα
είναι συνεχής στο διάστημα ![\displaystyle \left [ \frac{\pi }{4},\frac{\pi }{3} \right ] \displaystyle \left [ \frac{\pi }{4},\frac{\pi }{3} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/6de52e12f7be1c9242b85a5315f93ad9.png) και
και ,
, .
. ώστε
ώστε  στο
στο  , άρα το παραπάνω
, άρα το παραπάνω  είναι μοναδικό.
είναι μοναδικό. , σχέση
, σχέση  . Άρα:
. Άρα:
 .
. . Επομένως:
. Επομένως: .
. η ζητούμενη σχέση ισχύει ως
η ζητούμενη σχέση ισχύει ως  .
. , από το θεώρημα μέσης τιμής για την
, από το θεώρημα μέσης τιμής για την ![\left [ \alpha ,\beta \right ] \left [ \alpha ,\beta \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/fde3a58cd13724142f31784549724352.png) , υπάρχει
, υπάρχει 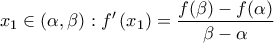 , δηλαδή:
, δηλαδή:


 για την οποία ισχύουν:
για την οποία ισχύουν:
 , για κάθε
, για κάθε  , για κάθε
, για κάθε  ισχύει
ισχύει  .
. και
και  το σημείο τομής τής εφαπτομένης της
το σημείο τομής τής εφαπτομένης της  , με τον άξονα
, με τον άξονα  . Αν τα παραπάνω σημεία σχηματίζουν τρίγωνο εμβαδού
. Αν τα παραπάνω σημεία σχηματίζουν τρίγωνο εμβαδού  τετραγωνικές μονάδες, να προσδιορίσετε την τιμή του
τετραγωνικές μονάδες, να προσδιορίσετε την τιμή του  .
. που είναι η παράγουσα της
που είναι η παράγουσα της  , όπου
, όπου  . Να βρείτε τη συνάρτηση
. Να βρείτε τη συνάρτηση  έχει ακριβώς τρεις ρίζες στο
έχει ακριβώς τρεις ρίζες στο  .
.
 , για κάθε
, για κάθε  τότε, να δείξετε ότι οι
τότε, να δείξετε ότι οι  δεν έχουν κοινά σημεία.
δεν έχουν κοινά σημεία. έχει ακριβώς μία ρίζα.
έχει ακριβώς μία ρίζα. η ρίζα της παραπάνω εξίσωσης, να υπολογίσετε το
η ρίζα της παραπάνω εξίσωσης, να υπολογίσετε το  .
.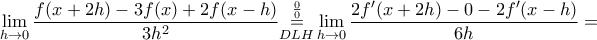
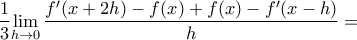
![\displaystyle{\frac{1}{3}\left[ \underset{h\to 0}{\mathop{\lim }}\,2\frac{{f}'(x+2h)-{f}'(x)}{2h}+\frac{{f}'(x-h)-{f}'(x)}{-h} \right]=} \displaystyle{\frac{1}{3}\left[ \underset{h\to 0}{\mathop{\lim }}\,2\frac{{f}'(x+2h)-{f}'(x)}{2h}+\frac{{f}'(x-h)-{f}'(x)}{-h} \right]=}](/forum/ext/geomar/texintegr/latexrender/pictures/812b5ac50ec88e496d2d800b25ede7d0.png)
![\displaystyle{\frac{1}{3}\left[ 2{f}''(x)+{f}''(x) \right]={f}''(x)} \displaystyle{\frac{1}{3}\left[ 2{f}''(x)+{f}''(x) \right]={f}''(x)}](/forum/ext/geomar/texintegr/latexrender/pictures/bc09fba7b57a7a9337f9084ebcf2cd46.png) επομένως η αρχική σχέση γίνεται
επομένως η αρχική σχέση γίνεται  οπότε
οπότε  ή
ή  (1)
(1) 
 ισχύει ότι
ισχύει ότι 
 λόγω Fermat είναι
λόγω Fermat είναι  και από (1) προκύπτει και λόγω του
και από (1) προκύπτει και λόγω του 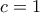 επομένως ισχύει ότι
επομένως ισχύει ότι  (2) άρα και με όπου
(2) άρα και με όπου  ισχύει ότι
ισχύει ότι (3) και με αφαίρεση κατά μέλη προκύπτει ότι
(3) και με αφαίρεση κατά μέλη προκύπτει ότι  ή
ή  άρα
άρα  και επειδή
και επειδή  και από (2) τότε
και από (2) τότε  επομένως
επομένως  και επειδή
και επειδή  που επαληθεύει την αρχική σχέση.
που επαληθεύει την αρχική σχέση. άρα
άρα  και επειδή
και επειδή 
 άρα
άρα 
 είναι γνήσια αύξουσα η
είναι γνήσια αύξουσα η  εκτός του σημείου επαφής, δηλαδή την ευθεία
εκτός του σημείου επαφής, δηλαδή την ευθεία  και θα ισχύει ότι
και θα ισχύει ότι  και επειδή ως γνωστόν ισχύει
και επειδή ως γνωστόν ισχύει 
 θα έχουμε ότι
θα έχουμε ότι  δηλαδή ισχύει ότι
δηλαδή ισχύει ότι  άρα οι
άρα οι  .
.![g(x)=\int\limits_{1}^{x}{4}tf(t)dt+\int\limits_{1}^{{{x}^{2}}}{f}(t)dt=2\int\limits_{1}^{x}{(}{{t}^{2}}{)}'f(t)dt+\left[ F(t) \right]_{1}^{{{x}^{2}}}= g(x)=\int\limits_{1}^{x}{4}tf(t)dt+\int\limits_{1}^{{{x}^{2}}}{f}(t)dt=2\int\limits_{1}^{x}{(}{{t}^{2}}{)}'f(t)dt+\left[ F(t) \right]_{1}^{{{x}^{2}}}=](/forum/ext/geomar/texintegr/latexrender/pictures/2f0b03b8d8181d39689e54109807eab9.png)
![\displaystyle{=2{{x}^{2}}\ln x-\left[ {{t}^{2}} \right]_{1}^{x}+F({{x}^{2}})-1=2{{x}^{2}}\ln x-{{x}^{2}}+1+F({{x}^{2}})-1\Leftrightarrow } \displaystyle{=2{{x}^{2}}\ln x-\left[ {{t}^{2}} \right]_{1}^{x}+F({{x}^{2}})-1=2{{x}^{2}}\ln x-{{x}^{2}}+1+F({{x}^{2}})-1\Leftrightarrow }](/forum/ext/geomar/texintegr/latexrender/pictures/d6bc1beb3f36001b004fd81c453777ed.png)
 είναι παραγωγίσιμη με
είναι παραγωγίσιμη με άρα
άρα 
 παρουσιάζει ελάχιστο στο
παρουσιάζει ελάχιστο στο  το
το  άρα το
άρα το 
 αφού
αφού 
![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) και τέτοια ώστε;
και τέτοια ώστε; για κάθε
για κάθε ![x\in [0,1] x\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/c628ba2b1047de93f66cb815d986e107.png)

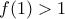
 τέτοιο ώστε
τέτοιο ώστε 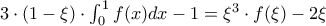 .
. ορισμένη στο
ορισμένη στο ![\left[0,1 \right] \left[0,1 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/7677ea85fbaa1efa02fd80baa7e802de.png)
 παραγωγίσιμη στο
παραγωγίσιμη στο 


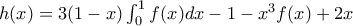 η οποία πληροί τις προυποθέσεις του
η οποία πληροί τις προυποθέσεις του  στο
στο 
