 . Όμως το
. Όμως το  μπορεί να είναι κάποιο απ΄τα
μπορεί να είναι κάποιο απ΄τα 
Σχετικά με το (γ) και (δ) εδώ και εδώ
Συντονιστές: m.pαpαgrigorakis, Καρδαμίτσης Σπύρος, Πρωτοπαπάς Λευτέρης, R BORIS, KAKABASBASILEIOS, Μπάμπης Στεργίου
Ζητώ τη συνέχεια της πρώτης παραγώγου, για το ερώτημα β) της άσκησης.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:ΑΣΚΗΣΗ 57
Γράφτηκε:
Για τα υπόλοιπα χρειάζεται νομίζω και η γνώση της συνέχειας της πρώτης παραγώγου της f.
Grosrouvre Δημοσιεύσεις: 209Εγγραφή: Τρί. Ιούλ. 15, 2014 10:37 pm
Η συνέχεια της παραγώγου δεν χρειάζεται.
Στο δ) πρέπει να προστεθεί ότι τα τρία σημεία δεν ταυτίζονται γιατί έτσι όπως είναι είναι τετριμένο.
ΛΥΣΗTolaso J Kos έγραψε:Άσκηση 54 (ρυθμός μεταβολής)
Έστω συνάρτησηπαραγωγίσιμη στο
. Θεωρούμε τη συνάρτηση
.
α) Να δείξετε ότι ηείναι παραγωγίσιμη στο
.
β) Αν είναινα βρείτε την εξίσωση εφαπτομένης της
στο σημείο
.
γ) Σημείοκινείται επί της προηγούμενης ευθείας και πλησιάζει τον άξονα
με ρυθμό
. Να βρείτε το ρυθμό μεταβολής της ελάχιστης απόστασης
τη χρονική κατά την οποία το
διέρχεται από το σημείο με τεταγμένη
.
 .
. είναι
είναι 




 παραγωγίσιμη στο
παραγωγίσιμη στο  με
με 
 θα είναι
θα είναι  και
και 
 στο σημείο
στο σημείο  είναι
είναι 
 και επειδή
και επειδή  είναι
είναι  και επειδή το μέγεθος
και επειδή το μέγεθος  μεταβάλλεται συναρτήσει του χρόνου
μεταβάλλεται συναρτήσει του χρόνου  αφού το μέγεθος μικραίνει επειδή πλησιάζει την αρχή των αξόνων θα είναι
αφού το μέγεθος μικραίνει επειδή πλησιάζει την αρχή των αξόνων θα είναι  και θέλουμε το
και θέλουμε το  όταν
όταν  .
.
 και επειδή
και επειδή 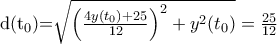 είναι
είναι 
Για να μην μείνε μετέωρη η παραπάνω συζήτηση αναφορικά με την Άσκηση 57, ας συμπληρώσω ότι παραμένω στην προηγούμενη τοποθέτησή μου αναφορικά με τους στόχους και τις επιδιώξεις του συγκεκριμένου φακέλου.Grosrouvre έγραψε:Ζητώ τη συνέχεια της πρώτης παραγώγου, για το ερώτημα β) της άσκησης.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:ΑΣΚΗΣΗ 57
Γράφτηκε:
Για τα υπόλοιπα χρειάζεται νομίζω και η γνώση της συνέχειας της πρώτης παραγώγου της f.
Grosrouvre Δημοσιεύσεις: 209Εγγραφή: Τρί. Ιούλ. 15, 2014 10:37 pm
Η συνέχεια της παραγώγου δεν χρειάζεται.
Στο δ) πρέπει να προστεθεί ότι τα τρία σημεία δεν ταυτίζονται γιατί έτσι όπως είναι είναι τετριμένο.
 , παραγωγίσιμη, με
, παραγωγίσιμη, με  και
και 
 και
και 


 για την οποία ισχύει
για την οποία ισχύει  ,
, , είναι η
, είναι η 
 για κάθε
για κάθε 
 του ερωτήματος 3, ισχύει:
του ερωτήματος 3, ισχύει: 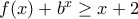
 , να δείξετε ότι
, να δείξετε ότι 
erxmer έγραψε:ΑΣΚΗΣΗ 58
Δίνεται συνάρτηση, παραγωγίσιμη, με
και
για κάθεκαι
1) Να δείξετε ότι
2) Να βρείτε την ελάχιστη τιμή της συνάρτησης
3) Να δείξετε ότι η μεγαλύτερη τιμή τουγια την οποία ισχύει
,
για κάθε, είναι η
4) Να δείξετε ότιγια κάθε
5) Αν για την τιμή τουτου ερωτήματος 3, ισχύει:
για κάθε, να δείξετε ότι


 σταθερή ,έστω
σταθερή ,έστω 
 είναι
είναι  άρα
άρα 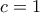
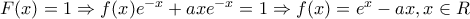

 είναι
είναι 
 είναι
είναι 

 ολικό ελάχιστο.
ολικό ελάχιστο. με
με  και η ζητόυμενη γίνεται
και η ζητόυμενη γίνεται 
 γν αύξουσα στο
γν αύξουσα στο ![(0,1] (0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/668c7b55a37300c330dcd565d9e076da.png) με
με ![g((0,1])=(0,1] g((0,1])=(0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/41ff2f28a631b8db2ff671aeffa39a26.png) και
και  γν φθίνουσα στο
γν φθίνουσα στο  με
με ![g({1,+\infty))=(-\infty,1] g({1,+\infty))=(-\infty,1]](/forum/ext/geomar/texintegr/latexrender/pictures/c2484075cb236890ab7f787281d76994.png)
 στο
στο ![(0,1] (0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/668c7b55a37300c330dcd565d9e076da.png) δεν έχει ρίζες ενώ στο
δεν έχει ρίζες ενώ στο  έχει μοναδική ρίζα το
έχει μοναδική ρίζα το  (προφανής ρίζα ,
(προφανής ρίζα ,  γν.μονότονη)
γν.μονότονη)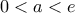 είναι
είναι  άρα η
άρα η  γίνεται
γίνεται 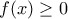 και δεν μπορεί να πάρει την τιμή
και δεν μπορεί να πάρει την τιμή 
 είναι
είναι  και πάλι η
και πάλι η  γίνεται
γίνεται 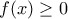 και δεν μπορεί να πάρει την τιμή
και δεν μπορεί να πάρει την τιμή 
 είναι
είναι  και η
και η  γίνεται
γίνεται 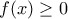 η οποία ισχύει για κάθε
η οποία ισχύει για κάθε 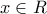 με
με 

![[x-2015,x] [x-2015,x]](/forum/ext/geomar/texintegr/latexrender/pictures/5bdbfc2ad1fc23df9c95a703ada280e3.png) και
και ![[x,2015+x] [x,2015+x]](/forum/ext/geomar/texintegr/latexrender/pictures/c2b00d7b478d659ab87f4aa8af191bcc.png) ,υπάρχουν
,υπάρχουν  ώστε
ώστε  ,
, άρα
άρα  γν. αυξουσα άρα
γν. αυξουσα άρα 

 και
και 
 , οπότε
, οπότε  ελάχιστο της
ελάχιστο της  και από Θ.Fermat
και από Θ.Fermat 
 για το οποίο ισχύει ότι
για το οποίο ισχύει ότι  . Να δείξετε ότι υπάρχει μία τουλάχιστον ρίζα του πολυωνύμου στο
. Να δείξετε ότι υπάρχει μία τουλάχιστον ρίζα του πολυωνύμου στο  .
. . Δείξτε ότι τα σημεία στα οποία η
. Δείξτε ότι τα σημεία στα οποία η  παρουσιάζει ακρότατα και καμπή εκτός του
παρουσιάζει ακρότατα και καμπή εκτός του  είναι κορυφές παραλληλογράμμου καθώς επίσης και ότι οι εφαπτομένες της
είναι κορυφές παραλληλογράμμου καθώς επίσης και ότι οι εφαπτομένες της  στα σημεία που παρουσιάζει καμπή τέμνονται σε σταθερή υπερβολή.
στα σημεία που παρουσιάζει καμπή τέμνονται σε σταθερή υπερβολή.
Καλησπέρα Απόστολε! Όμορφη άσκηση!Tolaso J Kos έγραψε:Άσκηση 59 (από τις σημειώσεις του Ροδόλφου)
Δίδεται πολυώνυμογια το οποίο ισχύει ότι
. Να δείξετε ότι υπάρχει μία τουλάχιστον ρίζα του πολυωνύμου στο
.
 για το οποίο ισχύει
για το οποίο ισχύει  .
. και
και  .
. ως πολυώνυμο είναι συνεχής συνάρτηση στο
ως πολυώνυμο είναι συνεχής συνάρτηση στο ![[0, 1] [0, 1]](/forum/ext/geomar/texintegr/latexrender/pictures/264884439b70ab09a86bc848421c6de6.png) και παραγωγίσιμη στο
και παραγωγίσιμη στο  ) προκύπτει το ζητούμενο.
) προκύπτει το ζητούμενο.Για την ιστορία, ας αναφερθεί ότι το θέμα αυτό το βρίσκουμε στο κλασικό βιβλίο του G.H. Hardy, A Course of Pure Mathematics, ως ένα θέμα από το Mathematical Tripos του έτους 1929.Tolaso J Kos έγραψε:Άσκηση 59 (από τις σημειώσεις του Ροδόλφου)
Δίδεται πολυώνυμογια το οποίο ισχύει ότι
. Να δείξετε ότι υπάρχει μία τουλάχιστον ρίζα του πολυωνύμου στο
.
Θάνο, ευχαριστούμε για τις πληροφορίες.matha έγραψε: Για την ιστορία, ας αναφερθεί ότι το θέμα αυτό το βρίσκουμε στο κλασικό βιβλίο του G.H. Hardy, A Course of Pure Mathematics, ως ένα θέμα από το Mathematical Tripos του έτους 1929.

ΑΣΚΗΣΗ 57ΈφηΚα έγραψε:Μπορεί κάποιο μέλος του, να λύσει παρακαλώ πολύ, την άσκηση 57. Ευχαριστώ!
 , με
, με  και η παραγωγίσιμη συνάρτηση
και η παραγωγίσιμη συνάρτηση  , για την οποία ισχύουν
, για την οποία ισχύουν  και
και  , για κάθε
, για κάθε ![x\in [\alpha ,\beta ] x\in [\alpha ,\beta ]](/forum/ext/geomar/texintegr/latexrender/pictures/1b7e1de5854145338ea14e58310eda48.png) . Αν τα σημεία
. Αν τα σημεία  ,
,  και
και  είναι συνεθειακά, τότε:
είναι συνεθειακά, τότε: .
. είναι γνησίως αύξουσα στο διάστημα
είναι γνησίως αύξουσα στο διάστημα ![[\alpha ,\beta ] [\alpha ,\beta ]](/forum/ext/geomar/texintegr/latexrender/pictures/13ac621dab037fd260a54755bb2382a3.png) .
. τέτοιο, ώστε
τέτοιο, ώστε  .
. τέτοια ώστε
τέτοια ώστε 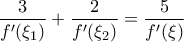 .
. συνάρτηση
συνάρτηση  με τις ιδιότητες :
με τις ιδιότητες : , για κάθε
, για κάθε  και
και  .
. είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  .
. καθώς και το
καθώς και το  .
. ,
,  .
. .
.![f''(x)=-2x[f'(x)]^{2} f''(x)=-2x[f'(x)]^{2}](/forum/ext/geomar/texintegr/latexrender/pictures/48c9c91e0013d1002203b8a4be607762.png) , για κάθε
, για κάθε  .
. , με
, με ![h(x)= \int_{1}^{x} [f'(t)]^{2} dt h(x)= \int_{1}^{x} [f'(t)]^{2} dt](/forum/ext/geomar/texintegr/latexrender/pictures/7b0979ffebbc4307d138c3da16da77de.png) και τις ευθείες με εξισώσεις
και τις ευθείες με εξισώσεις  ,
,  και
και  .
.Για το (α) απαίτησε τα διανύσματα.ΈφηΚα έγραψε:Γεια σας κ. Θάνο, επειδή γράφω από κινητό θα είμαι σύντομη! Το πρώτο ερώτημα δε ξέρω πως να το διαχειριστώ και στο δεύτερο νομίζω, βγαίνει με darboux αλλά δεν είμαι σίγουρη.
 και
και  να είναι παράλληλα . (ορίζουσα ίση με μηδέν)
να είναι παράλληλα . (ορίζουσα ίση με μηδέν) συνεχή. Ο θεματοδότης δεν βλέπω να το έχει σκοπό.
συνεχή. Ο θεματοδότης δεν βλέπω να το έχει σκοπό. .
.
 αντιστρέφεται και να βρείτε το πεδίο ορισμού της αντιστρόφου.
αντιστρέφεται και να βρείτε το πεδίο ορισμού της αντιστρόφου. είναι συνεχής να δείξετε ότι είναι και παραγωγίσιμη με παράγωγο
είναι συνεχής να δείξετε ότι είναι και παραγωγίσιμη με παράγωγο  .
.
 τότε να υπολογίσετε το ολοκλήρωμα
τότε να υπολογίσετε το ολοκλήρωμα 

...ΚαλησπέραTolaso J Kos έγραψε:Άσκηση 62 (προέκυψε από ένα θέμα του Θάνου εδώ στο)
Έστω η συνάρτηση.
- Να δείξετε ότι η
αντιστρέφεται και να βρείτε το πεδίο ορισμού της αντιστρόφου.
- Δεδομένου ότι η
είναι συνεχής να δείξετε ότι είναι και παραγωγίσιμη με παράγωγο
.
- Να δείξετε ότι
- Εάν
τότε να υπολογίσετε το ολοκλήρωμα
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με
με  άρα είναι γνήσια αύξουσα στο
άρα είναι γνήσια αύξουσα στο 
 επομένως αντιστρέφεται με
επομένως αντιστρέφεται με  και επειδή θα είναι και συνεχής
και επειδή θα είναι και συνεχής  με
με 



 είναι παραγωγίσιμη με
είναι παραγωγίσιμη με  και επειδή
και επειδή  με όπου
με όπου  το
το  προκύπτει ότι
προκύπτει ότι  άρα είναι
άρα είναι 
 είναι παραγωγίσιμη με
είναι παραγωγίσιμη με 

 είναι σταθερή στο
είναι σταθερή στο  δηλαδή είναι
δηλαδή είναι  (1).
(1).  θα ισχύει από (1)
θα ισχύει από (1) 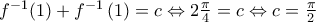
 .
. με
με  είναι
είναι  και
και  άρα
άρα 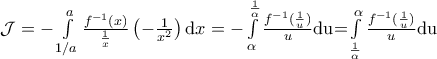 και λόγω (iii)
και λόγω (iii)  θα είναι
θα είναι ![\mathcal{J}=\int\limits_{\frac{1}{\alpha }}^{\alpha }{\frac{\frac{\pi }{2}-{{f}^{-1}}(x)}{x}}\text{dx=}\frac{\pi }{2}\int\limits_{\frac{1}{\alpha }}^{\alpha }{\frac{1}{x}}\text{dx-}\int\limits_{\frac{1}{\alpha }}^{\alpha }{\frac{{{f}^{-1}}(x)}{x}}\text{dx=}\frac{\pi }{2}\left[ \ln x \right]_{\frac{1}{\alpha }}^{\alpha }-\mathcal{J} \mathcal{J}=\int\limits_{\frac{1}{\alpha }}^{\alpha }{\frac{\frac{\pi }{2}-{{f}^{-1}}(x)}{x}}\text{dx=}\frac{\pi }{2}\int\limits_{\frac{1}{\alpha }}^{\alpha }{\frac{1}{x}}\text{dx-}\int\limits_{\frac{1}{\alpha }}^{\alpha }{\frac{{{f}^{-1}}(x)}{x}}\text{dx=}\frac{\pi }{2}\left[ \ln x \right]_{\frac{1}{\alpha }}^{\alpha }-\mathcal{J}](/forum/ext/geomar/texintegr/latexrender/pictures/5c716ff883071c0b85f43d2c9951f842.png) άρα
άρα 
για το ερώτημα (β)matha έγραψε:ΑΣΚΗΣΗ 57
Έστω, με
και η παραγωγίσιμη συνάρτηση
, για την οποία ισχύουν
και
, για κάθε
. Αν τα σημεία
,
και
είναι συνεθειακά, τότε:
α. Να δείξετε ότι.
β. Να δείξετε ότι η συνάρτησηείναι γνησίως αύξουσα στο διάστημα
.
γ. Να δείξετε ότι, υπάρχει μοναδικότέτοιο, ώστε
.
δ. Να δείξετε ότι υπάρχουντέτοια ώστε
.
 το δεξί μέλος θετικό απο υπόθεση, οπότε
το δεξί μέλος θετικό απο υπόθεση, οπότε 
 (απο το οποίο επίσης συμπεραίνεται ότι η
(απο το οποίο επίσης συμπεραίνεται ότι η  δεν είναι σταθερή)
δεν είναι σταθερή)![\displaystyle{ [\alpha,\beta ]} \displaystyle{ [\alpha,\beta ]}](/forum/ext/geomar/texintegr/latexrender/pictures/25cced110c10cd30cae3397c93a3c5aa.png) .
.![\displaystyle{ [\alpha,\beta ]} \displaystyle{ [\alpha,\beta ]}](/forum/ext/geomar/texintegr/latexrender/pictures/25cced110c10cd30cae3397c93a3c5aa.png) ως παραγωγίσιμη, οπότε απο θεώρημα μέγιστης και ελάχιστης τιμής η συνάρτηση θα πάρει μια μέγιστη τιμή και μια ελάχιστη. Εφ'όσον ισχύει
ως παραγωγίσιμη, οπότε απο θεώρημα μέγιστης και ελάχιστης τιμής η συνάρτηση θα πάρει μια μέγιστη τιμή και μια ελάχιστη. Εφ'όσον ισχύει  , έχει προφανώς ολικό ελάχιστο στο αριστερό άκρο και ολικό μέγιστο στο δεξί.
, έχει προφανώς ολικό ελάχιστο στο αριστερό άκρο και ολικό μέγιστο στο δεξί. τέτοια ώστε
τέτοια ώστε 
 τέτοιο ώστε
τέτοιο ώστε  , άτοπο.
, άτοπο. είναι γνησίως αύξουσα.
είναι γνησίως αύξουσα.Α.Αποστόλου έγραψε:για το ερώτημα (β)matha έγραψε:ΑΣΚΗΣΗ 57
Έστω, με
και η παραγωγίσιμη συνάρτηση
, για την οποία ισχύουν
και
, για κάθε
. Αν τα σημεία
,
και
είναι συνεθειακά, τότε:
α. Να δείξετε ότι.
β. Να δείξετε ότι η συνάρτησηείναι γνησίως αύξουσα στο διάστημα
.
γ. Να δείξετε ότι, υπάρχει μοναδικότέτοιο, ώστε
.
δ. Να δείξετε ότι υπάρχουντέτοια ώστε
.
από το (α ερώτημα)το δεξί μέλος θετικό απο υπόθεση, οπότε
Η συνάρτηση δεν παρουσιάζει τοπικά ακρότατα, καθότι(απο το οποίο επίσης συμπεραίνεται ότι η
δεν είναι σταθερή)
Επομένως τα σημεία των πιθανών της ακροτάτων είναι τα άκρα του.
Δεν είναι σταθερή και δεν έχει άλλα ακρότατα, άρα είναι μοναδικά. (αυτό το βρίσκω περιττό να διατυπωθεί)
Η συνάρτηση είναι συνεχής στοως παραγωγίσιμη, οπότε απο θεώρημα μέγιστης και ελάχιστης τιμής η συνάρτηση θα πάρει μια μέγιστη τιμή και μια ελάχιστη. Εφ'όσον ισχύει
, έχει προφανώς ολικό ελάχιστο στο αριστερό άκρο και ολικό μέγιστο στο δεξί.
δηλαδή είναι γνησίως αύξουσα.
Συμπλήρωση κατανόησης,αν είναι απλώς μονότονη τότε υπάρχουντέτοια ώστε
Οπότε απο το θεώρημα Rolle υπάρχειτέτοιο ώστε
, άτοπο.
Επομένως ηείναι γνησίως αύξουσα. Γιατί;; Πως προκύπτει το " γνησίως αύξουσα";;
(*)Ερώτηση προς βαθμολογητές πανελληνίων. Αν διαβάσετε συνεχής και "1-1", άρα γνησίως μονότοτονη, περιμένετε κάτι ακόμα ή είναι αρκετό;
Εφόσονrek2 έγραψε: Γιατί;; Πως προκύπτει το " γνησίως αύξουσα";;
 με
με 

 τέτοιο ώστε:
τέτοιο ώστε: 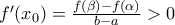
 με
με 
 τέτοιο ώστε
τέτοιο ώστε 
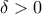 στο
στο  (δεν έχει σημασία η διάταξη) η παράγωγος δεν διατηρεί πρόσημο.
(δεν έχει σημασία η διάταξη) η παράγωγος δεν διατηρεί πρόσημο.  η συνάρτηση παρουσιάζει τοπικό ακρότατο.
η συνάρτηση παρουσιάζει τοπικό ακρότατο.  θα μηδενίστεί η παράγωγος, άτοπο.
θα μηδενίστεί η παράγωγος, άτοπο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες