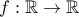 είναι δύο φορές παραγωγίσιμη και υπάρχει
είναι δύο φορές παραγωγίσιμη και υπάρχει  τέτοιο ώστε για κάθε
τέτοιο ώστε για κάθε 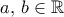 με
με  ισχύει
ισχύει 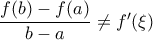
α) Βρείτε παράδειγμα τέτοιας συνάρτησης.
β) Δείξτε ότι
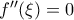 .
.Συντονιστές: m.pαpαgrigorakis, Καρδαμίτσης Σπύρος, Πρωτοπαπάς Λευτέρης, R BORIS, KAKABASBASILEIOS, Μπάμπης Στεργίου
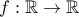 είναι δύο φορές παραγωγίσιμη και υπάρχει
είναι δύο φορές παραγωγίσιμη και υπάρχει  τέτοιο ώστε για κάθε
τέτοιο ώστε για κάθε 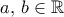 με
με  ισχύει
ισχύει 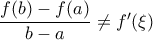
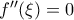 .
.α) ΗMihalis_Lambrou έγραψε: ↑Τρί Σεπ 26, 2023 9:20 amΜία συνάρτησηείναι δύο φορές παραγωγίσιμη και υπάρχει
τέτοιο ώστε για κάθε
με
ισχύει
α) Βρείτε παράδειγμα τέτοιας συνάρτησης.
β) Δείξτε ότι.
 . Για
. Για 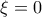 είναι
είναι 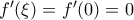 και
και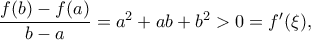
 , καθώς η ισότητα στην πιο πάνω ανισότητα ισχύει μόνο αν
, καθώς η ισότητα στην πιο πάνω ανισότητα ισχύει μόνο αν 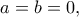 άτοπο.
άτοπο. ορίζουμε τη συνάρτηση
ορίζουμε τη συνάρτηση 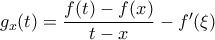 , με
, με 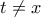 . Παρατηρούμε αρχικά ότι
. Παρατηρούμε αρχικά ότι 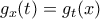 για κάθε
για κάθε  . Η συνάρτηση
. Η συνάρτηση  είναι διαφορετική του μηδενός για κάθε
είναι διαφορετική του μηδενός για κάθε  , και άρα διατηρεί πρόσημο σε καθένα από τα διαστήματα
, και άρα διατηρεί πρόσημο σε καθένα από τα διαστήματα  και
και 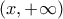 .
. διατηρεί σταθερό πρόσημο στο πεδίο ορισμού της, για κάθε
διατηρεί σταθερό πρόσημο στο πεδίο ορισμού της, για κάθε  .
. , για το οποίο η συνάρτηση
, για το οποίο η συνάρτηση 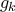 αλλάζει πρόσημο εκατέρωθεν του
αλλάζει πρόσημο εκατέρωθεν του  . Έστω, χωρίς βλάβη της γενικότητας, ότι η
. Έστω, χωρίς βλάβη της γενικότητας, ότι η 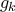 είναι αρνητική στο
είναι αρνητική στο 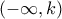 και θετική στο
και θετική στο 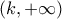 . Έστω επίσης
. Έστω επίσης  τέτοια ώστε
τέτοια ώστε 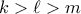 . Τότε,
. Τότε, 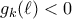 και
και 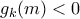 , συνεπώς και
, συνεπώς και 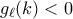 και
και 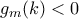 . Αυτό όμως σημαίνει ότι η συνάρτηση
. Αυτό όμως σημαίνει ότι η συνάρτηση 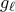 είναι αρνητική στο διάστημα
είναι αρνητική στο διάστημα 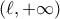 και ομοίως η συνάρτηση
και ομοίως η συνάρτηση 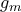 είναι αρνητική στο διάστημα
είναι αρνητική στο διάστημα  .
. 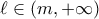 και
και 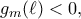 άρα
άρα 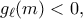 προκύπτει ότι η συνάρτηση
προκύπτει ότι η συνάρτηση 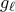 είναι αρνητική σε όλο το πεδίο ορισμού της.
είναι αρνητική σε όλο το πεδίο ορισμού της.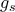 είναι θετική στο πεδίο ορισμού της, για κάθε
είναι θετική στο πεδίο ορισμού της, για κάθε 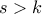 .
.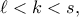 προκύπτει ότι
προκύπτει ότι 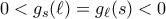 , άτοπο.
, άτοπο.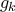 διατηρεί πρόσημο σε όλο το πεδίο ορισμού της, για κάθε
διατηρεί πρόσημο σε όλο το πεδίο ορισμού της, για κάθε 

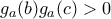 και
και 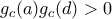
 διαφορετικά μεταξύ τους. Αφού όμως
διαφορετικά μεταξύ τους. Αφού όμως  προκύπτει ότι
προκύπτει ότι 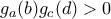 , συνεπώς η συνάρτηση δύο μεταβλητών
, συνεπώς η συνάρτηση δύο μεταβλητών 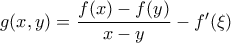 έχει σταθερό πρόσημο για κάθε
έχει σταθερό πρόσημο για κάθε  (αν κάποια από τα
(αν κάποια από τα  είναι ίσα μεταξύ τους, το ζητούμενο προκύπτει άμεσα από τα παραπάνω).
είναι ίσα μεταξύ τους, το ζητούμενο προκύπτει άμεσα από τα παραπάνω).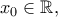
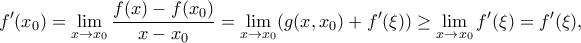
 παρουσιάζει στο
παρουσιάζει στο  ολικό ελάχιστο, άρα από το Θεώρημα Fermat
ολικό ελάχιστο, άρα από το Θεώρημα Fermat 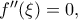 όπως θέλαμε.
όπως θέλαμε. έχει ολικό (άρα και τοπικό) ακρότατο στο
έχει ολικό (άρα και τοπικό) ακρότατο στο  . Αν δεν ισχύει αυτό, τότε μπορούμε να βρούμε
. Αν δεν ισχύει αυτό, τότε μπορούμε να βρούμε  ώστε
ώστε 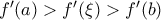 .
.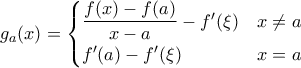
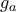 είναι παντού συνεχής (στο
είναι παντού συνεχής (στο  από την παραγωγισιμότητα της
από την παραγωγισιμότητα της  ) με
) με 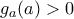 και
και 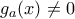 για
για 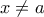 . Άρα η
. Άρα η 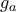 είναι παντού θετική. Ομοίως η
είναι παντού θετική. Ομοίως η 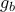 είναι παντού αρνητική. Αλλά τότε
είναι παντού αρνητική. Αλλά τότε  , άτοπο.
, άτοπο.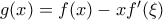 . H συνάρτηση αυτή είναι
. H συνάρτηση αυτή είναι  γιατί αλλιώς θα υπήρχαν
γιατί αλλιώς θα υπήρχαν  με
με 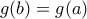 . Δηλαδή
. Δηλαδή 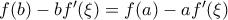 , ισοδύναμα
, ισοδύναμα 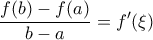 . Άτοπο.
. Άτοπο. είναι είτε αύξουσα ή φθίνουσα, ή αλλιώς
είναι είτε αύξουσα ή φθίνουσα, ή αλλιώς  για κάθε
για κάθε  , ή η ανάποδη ανισότητα. Ας πούμε, χωρίς βλάβη, ότι ισχύει η πρώτη, οπότε
, ή η ανάποδη ανισότητα. Ας πούμε, χωρίς βλάβη, ότι ισχύει η πρώτη, οπότε 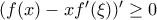 , ισόδύναμα
, ισόδύναμα 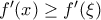 . Αυτό σημείναι ότι η
. Αυτό σημείναι ότι η  έχει ολικό ελάχιστο στο
έχει ολικό ελάχιστο στο  , οπότε
, οπότε 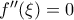 , όπως θέλαμε.
, όπως θέλαμε.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες