 , είναι η εικόνα του μιγαδικού
, είναι η εικόνα του μιγαδικού  , ενώ για τον μιγαδικό
, ενώ για τον μιγαδικό  ισχύει :
ισχύει :  .
.1) Βρείτε το γεωμετρικό τόπο των εικόνων του
 .
.2) Αν
 , είναι το σύνολο εκείνων από τους παραπάνω
, είναι το σύνολο εκείνων από τους παραπάνω  , για τους οποίους επιπλέον ισχύουν :
, για τους οποίους επιπλέον ισχύουν :
βρείτε ποιος , από τους ανήκοντες στο
 , βρίσκεται μακρύτερα του
, βρίσκεται μακρύτερα του  , και ποιος πλησιέστερα προς το
, και ποιος πλησιέστερα προς το  .
.Ντεφορμάρισμα : είναι Α(2,2)

 και
και  . Τότε, η δοσμένη σχέση γίνεται:
. Τότε, η δοσμένη σχέση γίνεται: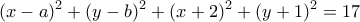 . Mετά από πράξεις...
. Mετά από πράξεις...


 . Aυτό σημαίνει ότι το Α υποχρεωτικά ανήκει στο εσωτερικό
. Aυτό σημαίνει ότι το Α υποχρεωτικά ανήκει στο εσωτερικό .
. και ακτίνα
και ακτίνα 

 με κέντρο
με κέντρο  και ακτίνα
και ακτίνα 
 .
. .
.
 και
και  . Άρα
. Άρα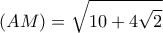 και
και 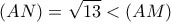 .
. και ο πιο
και ο πιο 




 ,
,  , άρα φτάνουμε στο
, άρα φτάνουμε στο 