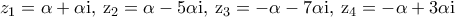
είναι ομοκυκλικά.
Συντονιστής: Πρωτοπαπάς Λευτέρης
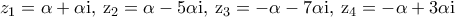

 τα σημεία ταυτίζονται. Για
τα σημεία ταυτίζονται. Για  , αρκεί να υπάρχουν
, αρκεί να υπάρχουν  με
με 
 επαληθεύεται από τις συντεταγμένες των τεσσάρων εικόνων.
επαληθεύεται από τις συντεταγμένες των τεσσάρων εικόνων. (1),
(1), 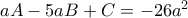 (2),
(2),  (3),
(3),  (4). Mε αφαίρεση των (1), (2) κατά μέλη έχουμε
(4). Mε αφαίρεση των (1), (2) κατά μέλη έχουμε . Mε πρόσθεση των (1), (3) κατά μέλη:
. Mε πρόσθεση των (1), (3) κατά μέλη: 
 . Oι τιμές αυτές επαληθεύουν την (4) και ισχύει
. Oι τιμές αυτές επαληθεύουν την (4) και ισχύει αφού
αφού  . Eπομένως, από τις εικόνες των τεσσάρων μιγαδικών
. Eπομένως, από τις εικόνες των τεσσάρων μιγαδικών , ο κύκλος
, ο κύκλος  που έχει κέντρο το
που έχει κέντρο το  και ακτίνα
και ακτίνα
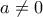 ) τα τέσσερα σημεία σχηματίζουν ισοσκελές τραπέζιο και είναι γνωστό ότι τα ισοσκελή τραπέζια είναι εγγράψιμα.
) τα τέσσερα σημεία σχηματίζουν ισοσκελές τραπέζιο και είναι γνωστό ότι τα ισοσκελή τραπέζια είναι εγγράψιμα.Demetres έγραψε:Αν δούμε το πρόβλημα γεωμετρικά, (για) τα τέσσερα σημεία σχηματίζουν ισοσκελές τραπέζιο και είναι γνωστό ότι τα ισοσκελή τραπέζια είναι εγγράψιμα.
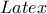 ;
; 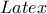 ;
; 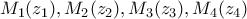 συνευθειακά , αρκεί :
συνευθειακά , αρκεί : * ( Titu Andreescu - Complex numbers from A to Z - καταπληκτικό βιβλίο)
* ( Titu Andreescu - Complex numbers from A to Z - καταπληκτικό βιβλίο) των μιγαδικών
των μιγαδικών  είναι συνευθειακά σημεία αν και μόνο αν
είναι συνευθειακά σημεία αν και μόνο αν  ".
". , άρα θα υπάρχει
, άρα θα υπάρχει 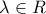 τέτοιο ώστε
τέτοιο ώστε  .
.Έστω οι μιγαδικοίκαι οι εικόνες τους
στο μιγαδικό επίπεδο. Να δείξετε ότι
συνευθειακά σημεία αν και μόνο αν
.
 , το ένα ζεύγος απέναντι πλευρών έχουν μήκη
, το ένα ζεύγος απέναντι πλευρών έχουν μήκη  και
και  αντίστοιχα, ενώ το άλλο ζεύγος απέναντι πλευρών έχουν και οι δύο μήκος
αντίστοιχα, ενώ το άλλο ζεύγος απέναντι πλευρών έχουν και οι δύο μήκος  . Οπότε επειδή
. Οπότε επειδή  τα σημεία είναι ομοκυκλικά.
τα σημεία είναι ομοκυκλικά. αρκεί να υπάρχει μιγάς
αρκεί να υπάρχει μιγάς 
 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες