Σελίδα 1 από 1
Διερεύνηση γεωμετρικού τόπου
Δημοσιεύτηκε: Πέμ Ιουν 20, 2013 5:54 pm
από thanasis kopadis
Να βρεθεί ο γεωμετρικός τόπος των εικόνων των μιγαδικών αριθμών

για τους οποίους ισχύει
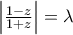
, για όλες τις τιμές του

.
Re: Διερεύνηση γεωμετρικού τόπου
Δημοσιεύτηκε: Πέμ Ιουν 20, 2013 7:13 pm
από Πρωτοπαπάς Λευτέρης
Καταρχήν για ευκολία στη γραφή χρησιμοποιώ
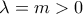
.
Για

και με

,
η δοσμένη σχέση ισοδύναμα γίνεται:


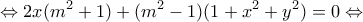

.
* Αν

έχουμε:

.
Τότε:

,
οπότε είναι κύκλος.
*Αν

η

δίνει:
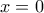
, δηλαδή είναι ο άξονας

.
Re: Διερεύνηση γεωμετρικού τόπου
Δημοσιεύτηκε: Πέμ Ιουν 20, 2013 7:17 pm
από BAGGP93
Καλησπέρα.
Θα πρέπει

Για

είναι,

Διακρίνουμε τις εξής περιπτώσεις για το

1)

Τότε, η
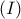
δίνει

2)

Θέτουμε

Αντικαθιστώντας στην
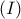
βρίσκουμε

Η παραπάνω εξίσωση παριστάνει κύκλο κέντρου

και ακτίνας

Re: Διερεύνηση γεωμετρικού τόπου
Δημοσιεύτηκε: Πέμ Ιουν 20, 2013 7:23 pm
από Σ. Διονύσης
Δε θα πρέπει και

?
Re: Διερεύνηση γεωμετρικού τόπου
Δημοσιεύτηκε: Πέμ Ιουν 20, 2013 7:30 pm
από Πρωτοπαπάς Λευτέρης
Σ. Διονύσης έγραψε:Δε θα πρέπει και

?
Αυτό δεν είναι απαίτηση για τη λύση, αφού με τις ισοδυναμίες και τις λύσεις δεν έχουμε θέμα.
Εξάλλου, ο συγκεκριμένος μιγαδικός δεν έχει εικόνα στον γεωμετρικό τόπο.
Re: Διερεύνηση γεωμετρικού τόπου
Δημοσιεύτηκε: Πέμ Ιουν 20, 2013 7:35 pm
από thanasis kopadis
Συνάδελφοι , ευχαριστώ πολύ. Μόλις κατάφερα κι εγώ να την ολοκληρώσω (θέλω προπόνηση στο Latex).

Και για να δώσω και την πηγή της άσκησης είναι από το βιβλίο του αείμνηστου Ν. Αρτεμιάδη, "Μιγαδική Ανάλυση".
Re: Διερεύνηση γεωμετρικού τόπου
Δημοσιεύτηκε: Πέμ Ιουν 20, 2013 7:37 pm
από Σ. Διονύσης
Πρωτοπαπάς Λευτέρης έγραψε:Σ. Διονύσης έγραψε:Δε θα πρέπει και

?
Αυτό δεν είναι απαίτηση για τη λύση, αφού με τις ισοδυναμίες και τις λύσεις δεν έχουμε θέμα.
Εξάλλου, ο συγκεκριμένος μιγαδικός δεν έχει εικόνα στον γεωμετρικό τόπο.
Kατάλαβα.Αλλά θα μπορούσε να δημιουργηθεί πρόβλημα σε άλλη άσκηση;
Re: Διερεύνηση γεωμετρικού τόπου
Δημοσιεύτηκε: Πέμ Ιουν 20, 2013 7:48 pm
από thanasis kopadis
Αγαπητέ Σ. Διονύση. Σκέψου ότι έχουμε να λύσουμε μια κλασματική ανίσωση, για παράδειγμα μεγαλύτερη του μηδενός. Αποκλείεται ο αριθμητής να είναι μηδέν. Όμως δεν το παίρνουμε στους περιορισμούς μας, αφού δεν πρόκειται να το γράψουμε έτσι κι αλλιώς στις λύσεις της ανίσωσης. Δεν ξέρω αν το παράδειγμα που σου έδωσα είναι εύστοχο, άλλα όπως το αντιλαμβάνομαι κάτι τέτοιο συμβαίνει και εδώ.
Re: Διερεύνηση γεωμετρικού τόπου
Δημοσιεύτηκε: Πέμ Ιουν 20, 2013 7:56 pm
από kostas_zervos
Για την ιστορία να σημειώσουμε το εξής:

- ask63.png (10.86 KiB) Προβλήθηκε 1038 φορές
Αν

και

η εικόνα του

, τότε

.
Αν

, τότε ο γεωμετρικός τόπος του

είναι ο Απολλώνιος κύκλος , δηλαδή ο κύκλος που έχει διάμετρο το

, όπου τα

ανήκουν στην ευθεία

και ισχύει ότι

(είναι δηλαδή συζυγή αρμονικά των

).
Στο παραπάνω σχήμα οι

είναι αντίστοιχα εσωτερική και εξωτερική διχοτόμος στο

.
Αν

, τότε

, άρα ο γεωμετρικός τόπος είναι η μεσοκάθετος του

.
 για τους οποίους ισχύει
για τους οποίους ισχύει 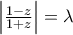 , για όλες τις τιμές του
, για όλες τις τιμές του  .
. για τους οποίους ισχύει
για τους οποίους ισχύει 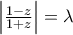 , για όλες τις τιμές του
, για όλες τις τιμές του  .
.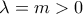 .
. και με
και με  ,
, 

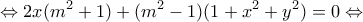
 .
. έχουμε:
έχουμε: .
. ,
, η
η  δίνει:
δίνει: 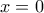 , δηλαδή είναι ο άξονας
, δηλαδή είναι ο άξονας  .
.
 είναι,
είναι,


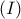 δίνει
δίνει 



 και ακτίνας
και ακτίνας 
 ?
? και
και  η εικόνα του
η εικόνα του  .
. , τότε ο γεωμετρικός τόπος του
, τότε ο γεωμετρικός τόπος του  , όπου τα
, όπου τα  ανήκουν στην ευθεία
ανήκουν στην ευθεία  και ισχύει ότι
και ισχύει ότι  (είναι δηλαδή συζυγή αρμονικά των
(είναι δηλαδή συζυγή αρμονικά των  ).
). είναι αντίστοιχα εσωτερική και εξωτερική διχοτόμος στο
είναι αντίστοιχα εσωτερική και εξωτερική διχοτόμος στο  .
. , τότε
, τότε  , άρα ο γεωμετρικός τόπος είναι η μεσοκάθετος του
, άρα ο γεωμετρικός τόπος είναι η μεσοκάθετος του