 , επαληθεύει την εξίσωση
, επαληθεύει την εξίσωση 
να αποδείξετε ότι

Συντονιστής: Πρωτοπαπάς Λευτέρης
Togradion έγραψε:Αν ο μιγαδικός, επαληθεύει την εξίσωση
να αποδείξετε ότι
 πρέπει να διορθωθεί σε
πρέπει να διορθωθεί σε ![[-2,2] [-2,2]](/forum/ext/geomar/texintegr/latexrender/pictures/98fab4cc523eb62bb9cf3a4fbefb7a69.png) όπως βλέπουμε από το παράδειγμα
όπως βλέπουμε από το παράδειγμα  . Όμοια το
. Όμοια το  πρέπει να διορθωθεί σε
πρέπει να διορθωθεί σε ![[-3,1] [-3,1]](/forum/ext/geomar/texintegr/latexrender/pictures/4129cdc3280d072f579d970ce058b667.png) , από το ίδιο παράδειγμα.
, από το ίδιο παράδειγμα. είναι
είναι  . Αντικατάσταση στην δοθείσα δίνει
. Αντικατάσταση στην δοθείσα δίνει
 δίνει
δίνει ![\frac {b}{a} = 2\cos \theta \in [-2, 2] \frac {b}{a} = 2\cos \theta \in [-2, 2]](/forum/ext/geomar/texintegr/latexrender/pictures/047b1f75190518c7f564bf3e6632a40d.png) .
.
 από όπου εύκολα
από όπου εύκολα ![\frac {c}{a} \in [-3, \, 1] \frac {c}{a} \in [-3, \, 1]](/forum/ext/geomar/texintegr/latexrender/pictures/5c8f0903f00a9dc01b4003957d771825.png)
 ή
ή  που έχει ρίζες
που έχει ρίζες 

 διαιρείται ακριβώς με το
διαιρείται ακριβώς με το 
 πρέπει να είναι το μηδενικό πολυώνυμο άρα
πρέπει να είναι το μηδενικό πολυώνυμο άρα  με
με  αφού
αφού  και
και 
 ,
,  οπότε καταλήγουμε στο ζητούμενο
οπότε καταλήγουμε στο ζητούμενο έχουμε την εξίσωση
έχουμε την εξίσωση  Αν
Αν  άμεσα παίρνουμε
άμεσα παίρνουμε  Με αντικατάσταση και λίγες πράξεις έχουμε:
Με αντικατάσταση και λίγες πράξεις έχουμε:  και
και  και βέβαια
και βέβαια  Αυτά αποτελούν και το ζητούμενο.
Αυτά αποτελούν και το ζητούμενο.
 έχουμε
έχουμε
 έχουμε:
έχουμε:
 Αν
Αν  τότε
τότε  άρα οι μιγαδικοί
άρα οι μιγαδικοί  και
και  ικανοποιούν την
ικανοποιούν την  . Άρα για
. Άρα για  έχω
έχω  και για
και για  έχω
έχω  απ' όπου με πρόσθεση κατά μέλη παίρνουμε
απ' όπου με πρόσθεση κατά μέλη παίρνουμε  δηλαδή
δηλαδή  και με αφαίρεση κατά μέλη παίρνουμε
και με αφαίρεση κατά μέλη παίρνουμε 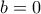 άρα
άρα  .
. Αν
Αν  τότε
τότε  άρα
άρα  συνεπώς
συνεπώς  και αφού
και αφού  παίρνουμε
παίρνουμε  και τελικά
και τελικά  .
. παίρνουμε
παίρνουμε  απ΄ όπου αντικαθιστώντας
απ΄ όπου αντικαθιστώντας  παίρνουμε
παίρνουμε  άρα
άρα  και αφού
και αφού  άρα τελικά
άρα τελικά ![\dfrac{c}{a}\in[-3,1] \dfrac{c}{a}\in[-3,1]](/forum/ext/geomar/texintegr/latexrender/pictures/8b58d525eeb68b9947f36045e788a719.png) .
. και
και  ανήκουν στα διαστήματα που ζητάει η εκφώνηση και έτσι η απόδειξη ολοκληρώθηκε.
ανήκουν στα διαστήματα που ζητάει η εκφώνηση και έτσι η απόδειξη ολοκληρώθηκε.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης