
 διέρχεται
διέρχεται1)από την αρχή
2)από το σημείο
 .
.Συντονιστής: Πρωτοπαπάς Λευτέρης

 διέρχεται
διέρχεται .
. ( με
( με  μια ρίζα είναι 0), ή, αν
μια ρίζα είναι 0), ή, αν  (έχουμε εκφυλισμένη περίπτωση με
(έχουμε εκφυλισμένη περίπτωση με  ), τότε ευθεία που ορίζεται από τις ρίζες
), τότε ευθεία που ορίζεται από τις ρίζες  διέρχεται από την αρχή
διέρχεται από την αρχή  .
. και
και  . Eίναι
. Eίναι  Η ευθεία που ορίζουν οι
Η ευθεία που ορίζουν οι  διέρχεται από την αρχή
διέρχεται από την αρχή  , αν και μόνο αν οι διανυσματικές ακτίνες τους είναι συγγραμμικές, δηλαδή αν και μόνο αν υπάρχει πραγματικός αριθμός
, αν και μόνο αν οι διανυσματικές ακτίνες τους είναι συγγραμμικές, δηλαδή αν και μόνο αν υπάρχει πραγματικός αριθμός  , τέτοιος ώστε
, τέτοιος ώστε  . Από αυτή τη σχέση και τις
. Από αυτή τη σχέση και τις  απαλείφουμε τα
απαλείφουμε τα  Η (2) λόγω της (1) δίνει
Η (2) λόγω της (1) δίνει , οπότε
, οπότε 
 , τώρα δίνει
, τώρα δίνει 
 οι
οι  δίνουν (εύκολο) την
δίνουν (εύκολο) την  και ισχύει το ζητούμενο.
και ισχύει το ζητούμενο. . Και οι δύο σχέσεις
. Και οι δύο σχέσεις  και
και  δίνουν
δίνουν 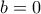 . Η αρχική εξίσωση έχει ρίζες αντίθετες (αυτές είναι συμμετρικές ως προς το
. Η αρχική εξίσωση έχει ρίζες αντίθετες (αυτές είναι συμμετρικές ως προς το  ,
,  δεν κείνται κατ΄ανάγκην στον άξονα των x
δεν κείνται κατ΄ανάγκην στον άξονα των x  ), οπότε η ευθεία που ορίζουν διέρχεται από το
), οπότε η ευθεία που ορίζουν διέρχεται από το  .
.  , ή,
, ή,  , ή, να υπάρχει πραγματικός
, ή, να υπάρχει πραγματικός  με
με 
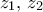 διέρχεται από την εικόνα του
διέρχεται από την εικόνα του  , αν και μόνο αν η ευθεία που ορίζουν οι
, αν και μόνο αν η ευθεία που ορίζουν οι  διέρχεται από την αρχή. Επομένως αναγόμαστε στην περίπτωση
διέρχεται από την αρχή. Επομένως αναγόμαστε στην περίπτωση  για τις ρίζες
για τις ρίζες  της εξίσωσης
της εξίσωσης  , όπου ορίσαμε
, όπου ορίσαμε  και
και 
 , ως ικανή και αναγκαία συνθήκη έχουμε:
, ως ικανή και αναγκαία συνθήκη έχουμε:  , ή,
, ή,  , ή, να υπάρχει πραγματικός
, ή, να υπάρχει πραγματικός  με
με 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες