 ισχύει:
ισχύει:
να βρεθεί ο :

Συντονιστής: Πρωτοπαπάς Λευτέρης
 \displaystyle{\displaystyle{7\frac{z}{{\bar{z}}}+\frac{{\bar{z}}}{z}-\frac{14}{{\bar{z}}}-\frac{2}{z}=-\frac{16}{\left| {{z}^{2}} \right|}\Leftrightarrow }
\displaystyle{\displaystyle{7\frac{z}{{\bar{z}}}+\frac{{\bar{z}}}{z}-\frac{14}{{\bar{z}}}-\frac{2}{z}=-\frac{16}{\left| {{z}^{2}} \right|}\Leftrightarrow } \displaystyle{\frac{7z-14}{{\bar{z}}}+\frac{\bar{z}-2}{z}=-\frac{16}{\left| {{z}^{2}} \right|}\Leftrightarrow }
\displaystyle{\frac{7z-14}{{\bar{z}}}+\frac{\bar{z}-2}{z}=-\frac{16}{\left| {{z}^{2}} \right|}\Leftrightarrow } \displaystyle{\frac{7(z-2)}{{\bar{z}}}+\frac{\bar{z}-2}{z}=-\frac{16}{\left| {{z}^{2}} \right|}}
\displaystyle{\frac{7(z-2)}{{\bar{z}}}+\frac{\bar{z}-2}{z}=-\frac{16}{\left| {{z}^{2}} \right|}} \displaystyle{\frac{z-2}{{\bar{z}}}=w}
\displaystyle{\frac{z-2}{{\bar{z}}}=w} \displaystyle{7w+\bar{w}=-\frac{16}{\left| {{z}^{2}} \right|}\Leftrightarrow }}
\displaystyle{7w+\bar{w}=-\frac{16}{\left| {{z}^{2}} \right|}\Leftrightarrow }} , άρα
, άρα 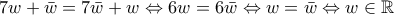 \displaystyle{\displaystyle{\Leftrightarrow \frac{z-2}{{\bar{z}}}=}}
\displaystyle{\displaystyle{\Leftrightarrow \frac{z-2}{{\bar{z}}}=}}
 \displaystyle{\displaystyle{{{z}^{2}}-{{\bar{z}}^{2}}-2z+2\bar{z}=0\Leftrightarrow (z-\bar{z})(z+\bar{z})-2(z-\bar{z})=0\Leftrightarrow }
\displaystyle{\displaystyle{{{z}^{2}}-{{\bar{z}}^{2}}-2z+2\bar{z}=0\Leftrightarrow (z-\bar{z})(z+\bar{z})-2(z-\bar{z})=0\Leftrightarrow } \displaystyle{\Leftrightarrow (z-\bar{z})(z+\bar{z}-2)=0\Leftrightarrow z=\bar{z}}
\displaystyle{\Leftrightarrow (z-\bar{z})(z+\bar{z}-2)=0\Leftrightarrow z=\bar{z}} \displaystyle{z+\bar{z}-2=0}
\displaystyle{z+\bar{z}-2=0} \displaystyle{\bullet }
\displaystyle{\bullet } \displaystyle{z=\bar{z}\Leftrightarrow z\in \mathbb{R}}
\displaystyle{z=\bar{z}\Leftrightarrow z\in \mathbb{R}} \displaystyle{7+1=\frac{14}{z}+\frac{2}{z}-\frac{16}{\left| {{z}^{2}} \right|}\Leftrightarrow 8=\frac{16z-16}{{{\left| z \right|}^{2}}}\Leftrightarrow 1=\frac{2z-2}{{{\left| z \right|}^{2}}}\Leftrightarrow }
\displaystyle{7+1=\frac{14}{z}+\frac{2}{z}-\frac{16}{\left| {{z}^{2}} \right|}\Leftrightarrow 8=\frac{16z-16}{{{\left| z \right|}^{2}}}\Leftrightarrow 1=\frac{2z-2}{{{\left| z \right|}^{2}}}\Leftrightarrow } \displaystyle{\overset{\left( z\in \mathbb{R} \right)}{\mathop{\Leftrightarrow }}\,\text{ }{{z}^{2}}-2z+2=0\Leftrightarrow {{\left( z-1 \right)}^{2}}+1=0}
\displaystyle{\overset{\left( z\in \mathbb{R} \right)}{\mathop{\Leftrightarrow }}\,\text{ }{{z}^{2}}-2z+2=0\Leftrightarrow {{\left( z-1 \right)}^{2}}+1=0} \displaystyle{\bullet }
\displaystyle{\bullet } \displaystyle{z+\bar{z}-2=0\Leftrightarrow 2\operatorname{Re}(z)=2\Leftrightarrow Re(z)=1}
\displaystyle{z+\bar{z}-2=0\Leftrightarrow 2\operatorname{Re}(z)=2\Leftrightarrow Re(z)=1} \displaystyle{z=1+yi,y\in \mathbb{R}}
\displaystyle{z=1+yi,y\in \mathbb{R}} \displaystyle{7w+\bar{w}=-\frac{16}{\left| {{z}^{2}} \right|}\overset{\left( w\in \mathbb{R} \right)}{\mathop{\Leftrightarrow }}\,8w=-\frac{16}{1+{{y}^{2}}}\Leftrightarrow w=-\frac{2}{1+{{y}^{2}}}}
\displaystyle{7w+\bar{w}=-\frac{16}{\left| {{z}^{2}} \right|}\overset{\left( w\in \mathbb{R} \right)}{\mathop{\Leftrightarrow }}\,8w=-\frac{16}{1+{{y}^{2}}}\Leftrightarrow w=-\frac{2}{1+{{y}^{2}}}} \displaystyle{\bullet }}
\displaystyle{\bullet }} \displaystyle{\displaystyle{\frac{-1+yi}{1-yi}=-\frac{2}{1+{{y}^{2}}}\Leftrightarrow }}
\displaystyle{\displaystyle{\frac{-1+yi}{1-yi}=-\frac{2}{1+{{y}^{2}}}\Leftrightarrow }}
 ,
,  , ομοίως και για
, ομοίως και για 

 οπότε
οπότε 



Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης