Σε απαιτητικούς μαθητές σκέφτομαι να την κάνω κάθε χρόνο, γιατι τρέμω στην ιδέα ότι θα τεθεί σοβαρό ερώτημα στις εξετάσεις και θα χαθεί από έλλειψη σωστής προετοιμασίας!
Να προσθέσω ότι δεν αποκλείεται να την έχω ξαναβάλει στο παρελθόν, μια και μερικές φορές βρίσκω την ίδια άσκηση σε διαφορετικές πηγές και την προσαρμόζω στα δικά μας μέτρα, χωρίς να θυμάμαι αν το έχω ξανακάνει!
Από ένα σημείο και μετά όλες οι ασκήσεις μοιάζουν - είναι και αυτό που με παιδεύει!!!
ΑΣΚΗΣΗ
Δίνεται συνάρτηση
 με πεδίο ορισμού το σύνολο
με πεδίο ορισμού το σύνολο  και την ιδιότητα:
και την ιδιότητα: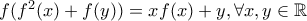 .
.Να αποδείξετε ότι:
α) Η συνάρτηση
 είναι
είναι  .
.β) Η
 έχει σύνολο τιμών το
έχει σύνολο τιμών το 
γ)

δ) Η
 αντιστρέφεται και
αντιστρέφεται και  .
.ε)

στ)
 ή
ή 

 για κάθε
για κάθε 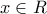
 για κάθε
για κάθε  για κάθε
για κάθε  για κάθε
για κάθε  για κάθε
για κάθε  για κάθε
για κάθε 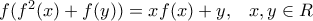 (1) και για
(1) και για  ότι
ότι  (2)
(2)  όταν ισχύει
όταν ισχύει  τότε και
τότε και  άρα και
άρα και 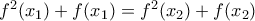 οπότε
οπότε  έτσι λόγω (2) θα ισχύει
έτσι λόγω (2) θα ισχύει  (3)
(3)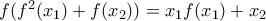 και
και 
 (4)
(4) άρα η
άρα η  και μοναδικό ώστε
και μοναδικό ώστε  οπότε από (2) θα ισχύει
οπότε από (2) θα ισχύει 
 από (1) ισχύει ότι
από (1) ισχύει ότι  ή
ή  οπότε για
οπότε για  το
το  λόγω του (β) θα ισχύει
λόγω του (β) θα ισχύει 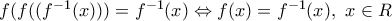
 και
και  θα ισχύει
θα ισχύει και λόγω του
και λόγω του  και επειδή για
και επειδή για  θα έχουμε τελικά ότι
θα έχουμε τελικά ότι  λόγω του (α)
λόγω του (α) τυχαίος, τότε για
τυχαίος, τότε για  ισχύει ότι
ισχύει ότι  .
. .
.![(\forall x\in\mathbb{R}) [f^2(x)=x^2] \iff (\forall x\in\mathbb{R}) [f^2(x)=x^2] \iff](/forum/ext/geomar/texintegr/latexrender/pictures/60c956fe56b7d31967ba522862a3289c.png)
 ή
ή ![f(x)=-x] f(x)=-x]](/forum/ext/geomar/texintegr/latexrender/pictures/8465147e1668239832a8e171d5640e5d.png)
 με
με  και
και 
 έχουμε:
έχουμε:
 ή
ή 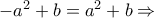
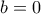 ή
ή  άτοπο.
άτοπο. ή
ή 
 .
.