 και
και  είναι συνεχείς στο
είναι συνεχείς στο  και για κάθε
και για κάθε 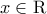 ισχύει
ισχύει  . Να αποδειχθεί ότι για κάθε
. Να αποδειχθεί ότι για κάθε 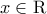 ισχύει
ισχύει  ή
ή  .
.Συντονιστής: m.pαpαgrigorakis
 και
και  είναι συνεχείς στο
είναι συνεχείς στο  και για κάθε
και για κάθε 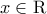 ισχύει
ισχύει  . Να αποδειχθεί ότι για κάθε
. Να αποδειχθεί ότι για κάθε 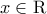 ισχύει
ισχύει  ή
ή  .
.Grosrouvre έγραψε:Δύο συναρτήσειςκαι
είναι συνεχείς στο
και για κάθε
ισχύει
. Να αποδειχθεί ότι για κάθε
ισχύει
ή
.
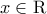 ισχύει
ισχύει  ή για κάθε
ή για κάθε 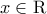 ισχύει
ισχύει  .
.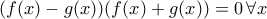 οπότε
οπότε 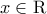 ισχύει
ισχύει  ή
ή  .
. δίνει
δίνει 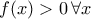 ή
ή  και όμοια για την
και όμοια για την  .
.  τότε έπεται για κάθε
τότε έπεται για κάθε  η
η  καθώς δεν υπάρχει
καθώς δεν υπάρχει  που ικανοποιεί την
που ικανοποιεί την  διότι τότε αυτό το
διότι τότε αυτό το  θα έδινε το άτοπο
θα έδινε το άτοπο  . Όμοια οι άλλες περιπτώσεις.
. Όμοια οι άλλες περιπτώσεις.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες