Δίνονται οι συναρτήσεις
 που είναι συνεχείς στο πεδίο ορισμού τους και έχουν σύνολο τιμών το
που είναι συνεχείς στο πεδίο ορισμού τους και έχουν σύνολο τιμών το  .
. Αν η
 είναι γνήσια αύξουσα και η
είναι γνήσια αύξουσα και η  γνήσια φθίνουσα να δειχθεί ότι οι
γνήσια φθίνουσα να δειχθεί ότι οι 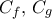 έχουν μοναδικό κοινό σημείο.
έχουν μοναδικό κοινό σημείο.Φιλικά και Μαθηματικά
Βασίλης
Συντονιστής: m.pαpαgrigorakis
 που είναι συνεχείς στο πεδίο ορισμού τους και έχουν σύνολο τιμών το
που είναι συνεχείς στο πεδίο ορισμού τους και έχουν σύνολο τιμών το  .
.  είναι γνήσια αύξουσα και η
είναι γνήσια αύξουσα και η  γνήσια φθίνουσα να δειχθεί ότι οι
γνήσια φθίνουσα να δειχθεί ότι οι 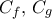 έχουν μοναδικό κοινό σημείο.
έχουν μοναδικό κοινό σημείο.Βασίλη καλό μεσημέριKAKABASBASILEIOS έγραψε:...Καλημέρασυνεχίζοντας γεωμετρικά....
Δίνονται οι συναρτήσειςπου είναι συνεχείς στο πεδίο ορισμού τους και έχουν σύνολο τιμών το
.
Αν ηείναι γνήσια αύξουσα και η
γνήσια φθίνουσα να δειχθεί ότι οι
έχουν μοναδικό κοινό σημείο.
Φιλικά και Μαθηματικά
Βασίλης

 .
. έχει μοναδική λύση ή ισοδύναμα ότι η εξίσωση
έχει μοναδική λύση ή ισοδύναμα ότι η εξίσωση  έχει μοναδική ρίζα ως προς
έχει μοναδική ρίζα ως προς  .
. για την οποία ισχύουν:
για την οποία ισχύουν:  η
η  είναι συνεχής στο
είναι συνεχής στο  (διαφορά συνεχών) και
(διαφορά συνεχών) και  η
η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  ,
,  ) άθροισμα γνησίως αυξουσών.
) άθροισμα γνησίως αυξουσών.


 που σημαίνει ότι
που σημαίνει ότι τέμνονται στο σημείο
τέμνονται στο σημείο  με
με  μοναδικό (άρα και
μοναδικό (άρα και  μοναδικό ) λόγω της γνήσιας μονοτονίας (γνησίως αύξουσα) της
μοναδικό ) λόγω της γνήσιας μονοτονίας (γνησίως αύξουσα) της 
 είναι το
είναι το  υπάρχει μοναδικό
υπάρχει μοναδικό  λόγω μονοτονίας ώστε
λόγω μονοτονίας ώστε 
 λόγω μονοτονίας ώστε
λόγω μονοτονίας ώστε 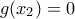
 προφανώς οι
προφανώς οι 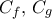 έχουν κοινό σημείο.
έχουν κοινό σημείο. , με
, με  η συνάρτηση
η συνάρτηση ![h(x)=f(x)-g(x),\,\,\,\,x\in [{{x}_{1}},\,\,{{x}_{2}}] h(x)=f(x)-g(x),\,\,\,\,x\in [{{x}_{1}},\,\,{{x}_{2}}]](/forum/ext/geomar/texintegr/latexrender/pictures/12bfb6d76979bc0e8742d917ccc86773.png) είναι συνεχής ως διαφορά συνεχών και
είναι συνεχής ως διαφορά συνεχών και  γιατί
γιατί  και
και  γνήσια φθίνουσα άρα
γνήσια φθίνουσα άρα 
 γιατί
γιατί  και
και  γνήσια αύξουσα άρα
γνήσια αύξουσα άρα  έτσι σύμφωνα με το θεώρημα του Bolzano υπάρχει
έτσι σύμφωνα με το θεώρημα του Bolzano υπάρχει  ώστε
ώστε 
 δείχνουμε ότι
δείχνουμε ότι  ώστε
ώστε  άρα σε κάθε περίπτωση οι οι
άρα σε κάθε περίπτωση οι οι 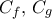 έχουν κοινό σημείο.
έχουν κοινό σημείο. είναι γνήσια αύξουσα (…εύκολα με τον ορισμό…) άρα και
είναι γνήσια αύξουσα (…εύκολα με τον ορισμό…) άρα και  επομένως η ρίζα της, είναι μοναδική.
επομένως η ρίζα της, είναι μοναδική.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες