Να βρεθούν όλες οι συνεχείς συναρτήσεις f που είναι λύσεις του συστήματος:
 ,
,
για κάθε θετικό
 .
.Έχω βρει πως από την πρώτη σχέση έχουμε πως η
 είναι
είναι  και έχω βρει πως μία (και λογικά η μοναδική) λύση είναι η
και έχω βρει πως μία (και λογικά η μοναδική) λύση είναι η  .
.Αντικαταστώντας στην 2η σχέση
 παίρνουμε
παίρνουμε  . Η
. Η  είναι 1-1 ,αφόυ η
είναι 1-1 ,αφόυ η  είναι 1-1 και είναι συνεχής ,αφού η
είναι 1-1 και είναι συνεχής ,αφού η  δεν μπορεί να μηδενίζεται λόγω της 2ης σχέσης και του ότι είναι 1-1.
δεν μπορεί να μηδενίζεται λόγω της 2ης σχέσης και του ότι είναι 1-1.Μένει να δείξω ότι
 αλλά δεν τα καταφέρνω παρότι μου φαίνεται εφικτό από την τελευταία σχέση.
αλλά δεν τα καταφέρνω παρότι μου φαίνεται εφικτό από την τελευταία σχέση.Θα εκτιμούσα οποιαδήποτε βοήθεια.

 την ικανοποιούν οι
την ικανοποιούν οι 
 την ικανοποιούν οι
την ικανοποιούν οι 
 . Δηλαδή η
. Δηλαδή η 

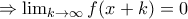 οπότε γενικά είναι
οπότε γενικά είναι 

 και γενικότερα
και γενικότερα 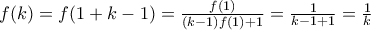
 για κάθε ρητό.
για κάθε ρητό. . Αν αυτό δεν ισχύει παίρνουμε το αντίστροφο και κάνουμε τα ίδια μ αυτά που ακολουθούν.
. Αν αυτό δεν ισχύει παίρνουμε το αντίστροφο και κάνουμε τα ίδια μ αυτά που ακολουθούν.  οπότε
οπότε  . Αυτό σημαίνει ότι αν
. Αυτό σημαίνει ότι αν  τότε
τότε 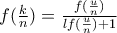
 .
. όπου
όπου  . Επαναλαμβάνουμε τα ίδια μέχρι που μετά από πεπερασμένο αριθμό βημάτων θα φτάσουμε στο να εξαρτώνται όλα τα προηγούμενα από ένα τελευταίο κλάσμα της μορφής
. Επαναλαμβάνουμε τα ίδια μέχρι που μετά από πεπερασμένο αριθμό βημάτων θα φτάσουμε στο να εξαρτώνται όλα τα προηγούμενα από ένα τελευταίο κλάσμα της μορφής  για το οποίο είναι
για το οποίο είναι  . Έτσι έχουμε
. Έτσι έχουμε  για κάθε ρητό.
για κάθε ρητό. με
με  οπότε λόγω συνεχείας είναι
οπότε λόγω συνεχείας είναι  αλλά
αλλά  οπότε
οπότε  για κάθε θετικό πραγματικό αριθμό.
για κάθε θετικό πραγματικό αριθμό.