 με
με  τέτοια ώστε
τέτοια ώστε (α) Να δειχθεί ότι η
(α) Να δειχθεί ότι η  αντιστρέφεται.
αντιστρέφεται.(β) Να δειχθεί ότι η (i) η
 είναι γνησίως αύξουσα και (ii) η
είναι γνησίως αύξουσα και (ii) η  είναι περιττή.
είναι περιττή.(γ) Να λυθεί η ανίσωση

Συντονιστής: m.pαpαgrigorakis
 με
με  τέτοια ώστε
τέτοια ώστε (α) Να δειχθεί ότι η
(α) Να δειχθεί ότι η  αντιστρέφεται.
αντιστρέφεται. είναι γνησίως αύξουσα και (ii) η
είναι γνησίως αύξουσα και (ii) η  είναι περιττή.
είναι περιττή.

Απλά και AN ο Αποστόλης ως εισηγητής ΔΕΝ έχει κάποια αντίρρηση, μπορεί να τεθεί και το επιπλέον ερώτημα:Tolaso J Kos έγραψε: ↑Τρί Ιούλ 11, 2023 10:39 pmΈστωμε
τέτοια ώστε
(α) Να δειχθεί ότι η
αντιστρέφεται.
(β) Να δειχθεί ότι η (i) ηείναι γνησίως αύξουσα και (ii) η
είναι περιττή.
(γ) Να λυθεί η ανίσωση
Καμία αντίρρηση Σωτήρη. Κουβέντα να γίνεται.S.E.Louridas έγραψε: ↑Πέμ Ιούλ 13, 2023 12:22 pmΑπλά και AN ο Αποστόλης ως εισηγητής ΔΕΝ έχει κάποια αντίρρηση, μπορεί να τεθεί και το επιπλέον ερώτημα:
Υπάρχει τέτοια συνάρτηση;
(*)
Και ένα of the record: Αν υπάρχει θα είναι επιπλέον αυτή συνεχής και παραγωγίσιμη;

α) Το α) εμπεριέχεται στο β) αφού, όπως θα αποδειχθεί, ηTolaso J Kos έγραψε: ↑Τρί Ιούλ 11, 2023 10:39 pmΈστωμε
τέτοια ώστε
(α) Να δειχθεί ότι η
αντιστρέφεται.
(β) Να δειχθεί ότι η (i) ηείναι γνησίως αύξουσα και (ii) η
είναι περιττή.
(γ) Να λυθεί η ανίσωση

 είναι γνήσια αύξουσα και άρα
είναι γνήσια αύξουσα και άρα  . Ουσιαστικά αυτό που θέλουμε είναι να δείξουμε ότι η
. Ουσιαστικά αυτό που θέλουμε είναι να δείξουμε ότι η  είναι
είναι  , γενικότερα, γνήσια αύξουσα συνάρτηση του
, γενικότερα, γνήσια αύξουσα συνάρτηση του  .
.  είναι γνήσια αύξουσα γιατί αν
είναι γνήσια αύξουσα γιατί αν  δεν μπορεί
δεν μπορεί  γιατί τότε
γιατί τότε  . Άτοπο.
. Άτοπο.  . Άρα
. Άρα  αφού η
αφού η  είναι
είναι  . Δηλαδή η
. Δηλαδή η  είναι περιττή.
είναι περιττή.  . Πράγματι, είναι
. Πράγματι, είναι  , οπότε
, οπότε  και άρα
και άρα  . Με χρήση αυτoύ και του γεγονότος ότι η
. Με χρήση αυτoύ και του γεγονότος ότι η  (οπότε και η
(οπότε και η  ) είναι γνήσια αύξουσες, έχουμε
) είναι γνήσια αύξουσες, έχουμε  ισχύει
ισχύει 
 .
. 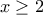 η ανίσωση δεν ικανοποιείται. Η ιδέα είναι παραλλαγή της προηγούμενης γραμμής:
η ανίσωση δεν ικανοποιείται. Η ιδέα είναι παραλλαγή της προηγούμενης γραμμής: 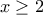 έχουμε
έχουμε  , δηλαδή η ανάποδη ανισότητα.
, δηλαδή η ανάποδη ανισότητα.ΘέτουμεS.E.Louridas έγραψε: ↑Πέμ Ιούλ 13, 2023 12:22 pm
... μπορεί να τεθεί και το επιπλέον ερώτημα:
Υπάρχει τέτοια συνάρτηση;
(*)
Και ένα of the record: Αν υπάρχει θα είναι επιπλέον αυτή συνεχής και παραγωγίσιμη;
 , η οποία αντιστρέφεται (το είδαμε). Έχουμε λοιπόν για κάθε
, η οποία αντιστρέφεται (το είδαμε). Έχουμε λοιπόν για κάθε  ότι
ότι  . Άρα
. Άρα  . Δηλαδή η
. Δηλαδή η  όχι μόνο υπάρχει, αλλά βρήκαμε και την μορφή της. Από αυτό έπεται και η απάντηση στο δεύτερο ερώτημα: Ναι είναι συνεχής ως αντίστροφη συνεχούς, και μάλιστα από θεωρία (πόρισμα του κανόνα αλυσίδας) είναι παραγωγίσιμη εκτός εκεί που μηδενίζεται η
όχι μόνο υπάρχει, αλλά βρήκαμε και την μορφή της. Από αυτό έπεται και η απάντηση στο δεύτερο ερώτημα: Ναι είναι συνεχής ως αντίστροφη συνεχούς, και μάλιστα από θεωρία (πόρισμα του κανόνα αλυσίδας) είναι παραγωγίσιμη εκτός εκεί που μηδενίζεται η  (εδώ
(εδώ  που δεν μηδενίζεται πουθενά).
που δεν μηδενίζεται πουθενά). και αφού η f είναι γνήσια αύξουσα
και αφού η f είναι γνήσια αύξουσα 
 άρα
άρα 


 άρα
άρα  οπότε η
οπότε η  γίνεται :
γίνεται : και επειδή η h είναι γνήσια αύξουσα
και επειδή η h είναι γνήσια αύξουσα 
Είναι όλα σωστά και καλά.

 και της γνήσια φθίνουσας
και της γνήσια φθίνουσας  . Άρα αν για κάποιο
. Άρα αν για κάποιο  έχουμε ισότητα
έχουμε ισότητα  , τότε εύκολα βλέπουμε ότι το σύνολο λύσεων είναι τα
, τότε εύκολα βλέπουμε ότι το σύνολο λύσεων είναι τα  . Όποτε ψάχνουμε ένα τέτοιο
. Όποτε ψάχνουμε ένα τέτοιο  . Με απλές δοκιμές βλέπουμε ότι το
. Με απλές δοκιμές βλέπουμε ότι το 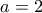 μας κάνει. Τελειώσαμε.
μας κάνει. Τελειώσαμε.Παντού είναι παραγωγίσιμη γιατίMihalis_Lambrou έγραψε: ↑Παρ Ιούλ 14, 2023 10:20 pmΘέτουμε, η οποία αντιστρέφεται (το είδαμε). Έχουμε λοιπόν για κάθε
ότι
. Άρα
. Δηλαδή η
όχι μόνο υπάρχει, αλλά βρήκαμε και την μορφή της. Από αυτό έπεται και η απάντηση στο δεύτερο ερώτημα: Ναι είναι συνεχής ως αντίστροφη συνεχούς, και μάλιστα από θεωρία (πόρισμα του κανόνα αλυσίδας) είναι παραγωγίσιμη εκτός εκεί που μηδενίζεται η
, δηλαδή (μόνο) στο
.

Σωστά. Έκανα διόρθωση στην αρχική μου απάντηση. Ευχαριστώ.
 , αντιστοιχίζεται
, αντιστοιχίζεται  αν υπάρχουν πάνω από μία ρίζες ή η μοναδική ρίζα αν δεν υπάρχει άλλη.
αν υπάρχουν πάνω από μία ρίζες ή η μοναδική ρίζα αν δεν υπάρχει άλλη.Σωτήρη, σωστά αλλά ας επισημάνω ότι: Υπάρχει μόνο μία τέτοια συνάρτηση (δεν έχουμε επιλογή). Επίσης, η εξίσωσηS.E.Louridas έγραψε: ↑Σάβ Ιούλ 15, 2023 5:14 pmΠάντως μία τέτοια συνάρτηση είναι εκείνη που στον τυχόντα πραγματικό, αντιστοιχίζεται
π.χ. η μεγαλύτερη από τις πραγματικές ρίζες της
 έχει ακριβώς μία ρίζα, οπότε δεν τίθεται θέμα να πάρουμε την μεγαλύτερη.
έχει ακριβώς μία ρίζα, οπότε δεν τίθεται θέμα να πάρουμε την μεγαλύτερη. Mihalis_Lambrou έγραψε: ↑Παρ Ιούλ 14, 2023 10:20 pm
Θέτουμε, η οποία αντιστρέφεται (το είδαμε). Έχουμε λοιπόν για κάθε
ότι
. Άρα
.
Προφανώς Σωστά, απλά είχα στο μυαλό μου τη γενικότερη κατάστασηMihalis_Lambrou έγραψε: ↑Σάβ Ιούλ 15, 2023 6:26 pmΣωτήρη, σωστά αλλά ας επισημάνω ότι: Υπάρχει μόνο μία τέτοια συνάρτηση (δεν έχουμε επιλογή). Επίσης, η εξίσωσηS.E.Louridas έγραψε: ↑Σάβ Ιούλ 15, 2023 5:14 pmΠάντως μία τέτοια συνάρτηση είναι εκείνη που στον τυχόντα πραγματικό, αντιστοιχίζεται
π.χ. η μεγαλύτερη από τις πραγματικές ρίζες της
έχει ακριβώς μία ρίζα, οπότε δεν τίθεται θέμα να πάρουμε την μεγαλύτερη.
Αυτά είναι ουσιαστικά γραμμένα στην απάντησή μου, στο σημείο:Mihalis_Lambrou έγραψε: ↑Παρ Ιούλ 14, 2023 10:20 pmΘέτουμε, η οποία αντιστρέφεται (το είδαμε). Έχουμε λοιπόν για κάθε
ότι
. Άρα
.
![k{\left[ {f\left( x \right)} \right]^{2n + 1}} + m\,f\left( x \right) = \ell x, k{\left[ {f\left( x \right)} \right]^{2n + 1}} + m\,f\left( x \right) = \ell x,](/forum/ext/geomar/texintegr/latexrender/pictures/78d1f61dcfc370c9b460967cdc2c0f59.png) με
με  πραγματικές σταθερές διάφορες του μηδέν (αν και θα μπορούσαμε να μπούμε και σε διερευνητική διαδικασία) αναφέροντας έτσι μία γενικότερη άποψη λύσης που λειτουργεί και εδώ χωρίς να χρειαστεί το 1-1. Ταυτόχρονα λειτουργεί και ο αρχικός ορισμός της έννοιας συνάρτηση ως ενός τρόπου ... Επειδή πιστεύω ότι είναι καλό να μη ξεχνάμε και τις στοιχειώδης αρχικές συμπεριφορές των μαθηματικών εννοιών και μεθόδων επίλυσης για ουσιαστικούς λόγους που θεωρώ ότι είναι κατανοητοί. Ο τρόπος βέβαια επίλυσης του Μιχάλη είναι ένας άριστος και ευφυής τρόπος επίλυσης, απλά εγώ αναφέρομαι στο σκεπτικό μου για τον λόγο που έθεσα τα επιπλέον ερωτήματα στο όμορφο πράγματι πρόβλημα που έθεσε ο Αποστόλης.
πραγματικές σταθερές διάφορες του μηδέν (αν και θα μπορούσαμε να μπούμε και σε διερευνητική διαδικασία) αναφέροντας έτσι μία γενικότερη άποψη λύσης που λειτουργεί και εδώ χωρίς να χρειαστεί το 1-1. Ταυτόχρονα λειτουργεί και ο αρχικός ορισμός της έννοιας συνάρτηση ως ενός τρόπου ... Επειδή πιστεύω ότι είναι καλό να μη ξεχνάμε και τις στοιχειώδης αρχικές συμπεριφορές των μαθηματικών εννοιών και μεθόδων επίλυσης για ουσιαστικούς λόγους που θεωρώ ότι είναι κατανοητοί. Ο τρόπος βέβαια επίλυσης του Μιχάλη είναι ένας άριστος και ευφυής τρόπος επίλυσης, απλά εγώ αναφέρομαι στο σκεπτικό μου για τον λόγο που έθεσα τα επιπλέον ερωτήματα στο όμορφο πράγματι πρόβλημα που έθεσε ο Αποστόλης.
 παίρνουμε
παίρνουμε [1]
[1] συνεχής [2]
συνεχής [2] παραγωγίσιμη [3]
παραγωγίσιμη [3] [4]
[4] [5]
[5] μοναδική ρίζα [6]
μοναδική ρίζα [6] [7]
[7] [8]
[8] [9]
[9] ,
, ο.ε.δ
ο.ε.δ ,
, επειδή
επειδή  το ζητουμενο ισχυει
το ζητουμενο ισχυει από [1]
από [1]  και δεδομένου ότι
και δεδομένου ότι  η
η  αντιστρεφεται στο R
αντιστρεφεται στο R
 \displaystyle{ ή }
\displaystyle{ ή } \displaystyle{ ή
\displaystyle{ ή  \displaystyle{,}
\displaystyle{,} \displaystyle{,}
\displaystyle{,} \displaystyle{που ισχυει αν θεσουμε }
\displaystyle{που ισχυει αν θεσουμε } \displaystyle{
\displaystyle{ \displaystyle{ από [1] ισχυει το ζητουμενο
\displaystyle{ από [1] ισχυει το ζητουμενο,y=f(x)} x=f^{-1](y),y=f(x)}](/forum/ext/geomar/texintegr/latexrender/pictures/fc7d5e135c5264938c41acab848ae419.png) \displaystyle{ και ετσι ισχυει η [9] σε ολο το R αφου }
\displaystyle{ και ετσι ισχυει η [9] σε ολο το R αφου } \displaystyle{
\displaystyle{ $ και εχει ρίζα το 2 αρα χ<2
$ και εχει ρίζα το 2 αρα χ<2Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες