 με
με 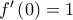 , για την οποία ισχύει
, για την οποία ισχύει 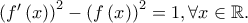
(α) Να αποδείξετε ότι η
 αντιστρέφεται και ότι είναι δύο φορές παραγωγίσιμη στο
αντιστρέφεται και ότι είναι δύο φορές παραγωγίσιμη στο  με
με 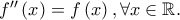
(β) Να βρείτε τον τύπο της

(γ) Να ορίσετε την αντίστροφη της

(δ) Να υπολογίσετε το ολοκλήρωμα
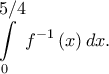
(ε) Να αποδείξετε ότι
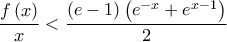 για κάθε
για κάθε 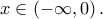
Συντονιστής: m.pαpαgrigorakis
 με
με 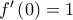 , για την οποία ισχύει
, για την οποία ισχύει 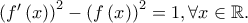
 αντιστρέφεται και ότι είναι δύο φορές παραγωγίσιμη στο
αντιστρέφεται και ότι είναι δύο φορές παραγωγίσιμη στο  με
με 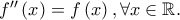


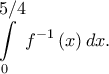
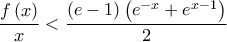 για κάθε
για κάθε 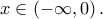
Παραθέτω μια προσπάθεια για αναλυτική λύση (για το (δ) δεν είμαι σίγουρος λόγω του αποτελέσματος). Σίγουρα υπάρχουν πιο σύντομες, ειδικά για την παραγωγισιμότητα τηςDimessi έγραψε: ↑Τρί Ιαν 02, 2024 12:46 pmΘεωρούμε την παραγωγίσιμη συνάρτησημε
, για την οποία ισχύει
(α) Να αποδείξετε ότι ηαντιστρέφεται και ότι είναι δύο φορές παραγωγίσιμη στο
με
(β) Να βρείτε τον τύπο της
(γ) Να ορίσετε την αντίστροφη της
(δ) Να υπολογίσετε το ολοκλήρωμα
(ε) Να αποδείξετε ότιγια κάθε
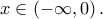
 στο (α).
στο (α).  δεν είναι 1-1. Τότε υπάρχουν
δεν είναι 1-1. Τότε υπάρχουν  με
με  τέτοια, ώστε
τέτοια, ώστε 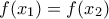 .
.![[x_1, x_2] [x_1, x_2]](/forum/ext/geomar/texintegr/latexrender/pictures/5c5098079470feacb4129bd5592df89e.png) , υπάρχει ένα, τουλάχιστον,
, υπάρχει ένα, τουλάχιστον, 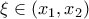 τέτοιο, ώστε
τέτοιο, ώστε  , άτοπο αφού
, άτοπο αφού 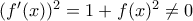 , για κάθε
, για κάθε  , οπότε
, οπότε 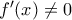 , για κάθε
, για κάθε 
 , είναι γνησίως μονότονη στο
, είναι γνησίως μονότονη στο  .
.  με
με  και
και 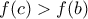 . Παίρνουμε κάποιο
. Παίρνουμε κάποιο  με
με 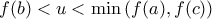 .
.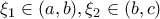 τέτοια, ώστε
τέτοια, ώστε 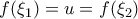 , που αντιβαίνει στο 1-1 της συνάρτησης.
, που αντιβαίνει στο 1-1 της συνάρτησης. 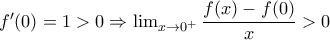 , οπότε κοντά στο
, οπότε κοντά στο 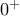 :
: 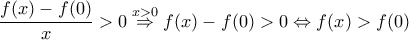 .
. ήταν γνησίως φθίνουσα, κοντά στο
ήταν γνησίως φθίνουσα, κοντά στο 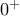 θα ήταν
θα ήταν 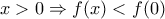 , άτοπο.
, άτοπο. είναι γνησίως αύξουσα. Με ανάλογο τρόπο έχουμε πως αν υπήρχε
είναι γνησίως αύξουσα. Με ανάλογο τρόπο έχουμε πως αν υπήρχε 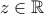 με
με 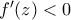 , τότε κοντά στο
, τότε κοντά στο 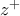 :
: 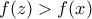 , άτοπο αφού
, άτοπο αφού 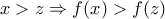 , οπότε
, οπότε 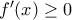 , για κάθε
, για κάθε  , και επειδή
, και επειδή 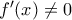 ,
,  , για κάθε
, για κάθε  .
.  .
. 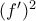 είναι παραγωγίσιμη (και συνεχής) στο
είναι παραγωγίσιμη (και συνεχής) στο  , οπότε
, οπότε 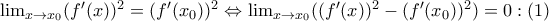 και
και 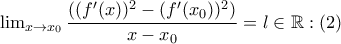 .
. είναι συνεχής, και στη συνέχεια ότι είναι παραγωγίσιμη.
είναι συνεχής, και στη συνέχεια ότι είναι παραγωγίσιμη.  ,
, 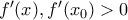 και (ας πούμε)
και (ας πούμε) 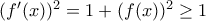 , θα είναι:
, θα είναι: 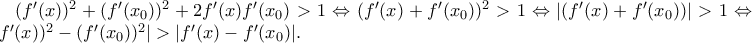
 από κριτήριο παρεμβολής παίρνουμε
από κριτήριο παρεμβολής παίρνουμε 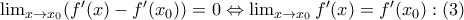
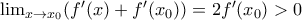 , άρα κοντά στο
, άρα κοντά στο  είναι
είναι 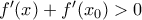 , οπότε:
, οπότε: 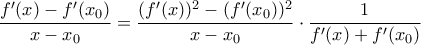 , άρα
, άρα 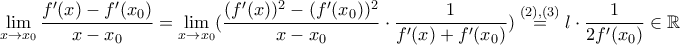
 είναι παραγωγίσιμη, δηλαδή η
είναι παραγωγίσιμη, δηλαδή η  είναι δύο φορές παραγωγίσιμη.
είναι δύο φορές παραγωγίσιμη. 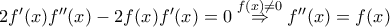 , για κάθε
, για κάθε  .
. 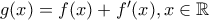 η οποία είναι παραγωγίσιμη με
η οποία είναι παραγωγίσιμη με 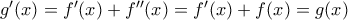 , για κάθε
, για κάθε  .
. 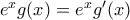 , άρα
, άρα 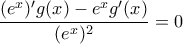 , ή
, ή 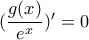 , για κάθε
, για κάθε  . Από συνέπειες ΘΜΤ:
. Από συνέπειες ΘΜΤ: 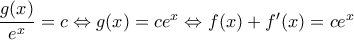 , για κάποιο
, για κάποιο  .
.  στην αρχική σχέση έχουμε
στην αρχική σχέση έχουμε  άρα
άρα 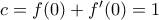 , οπότε
, οπότε 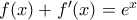 , για κάθε
, για κάθε  .
.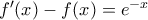 , για κάθε
, για κάθε  , και αφαιρώντας την τελευταία παίρνουμε
, και αφαιρώντας την τελευταία παίρνουμε 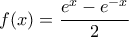 , για κάθε
, για κάθε  .
.  έχουμε
έχουμε 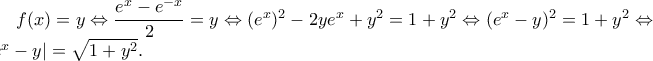
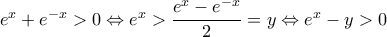 , άρα η εξίσωση γράφεται ισοδύναμα
, άρα η εξίσωση γράφεται ισοδύναμα 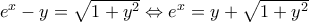 , η οποία (αφού
, η οποία (αφού 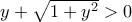 για κάθε
για κάθε  , που δείχνεται πχ με διατήρηση προσήμου) γράφεται ισοδύναμα
, που δείχνεται πχ με διατήρηση προσήμου) γράφεται ισοδύναμα 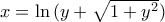 . Επειδή δεν προέκυψαν περιορισμοί για το
. Επειδή δεν προέκυψαν περιορισμοί για το  θα είναι
θα είναι 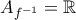 και
και 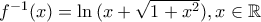 .
.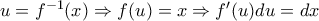 . Υπολογίζουμε τα άκρα ολοκλήρωσης:
. Υπολογίζουμε τα άκρα ολοκλήρωσης: 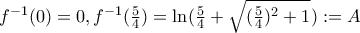 , άρα το ολοκλήρωμα ισούται με
, άρα το ολοκλήρωμα ισούται με ![\int\limits_{0}^{A}uf'(u)du = [uf(u)]^{A}_0 - \int\limits_{0}^{A}f(u)du = [uf(u)]^{A}_0 - [\dfrac{e^u+e^{-u}}{2}]^{A}_{0} = \frac{5A}{4} - \dfrac{e^A+e^{-A}}{2} = \frac{5A}{4}-\sqrt{((\frac{5}{4})^2+1)} \int\limits_{0}^{A}uf'(u)du = [uf(u)]^{A}_0 - \int\limits_{0}^{A}f(u)du = [uf(u)]^{A}_0 - [\dfrac{e^u+e^{-u}}{2}]^{A}_{0} = \frac{5A}{4} - \dfrac{e^A+e^{-A}}{2} = \frac{5A}{4}-\sqrt{((\frac{5}{4})^2+1)}](/forum/ext/geomar/texintegr/latexrender/pictures/3018bc4f4331edc41fba6fc3f3ca8676.png) .
.  είναι
είναι  άρα
άρα  , οπότε η
, οπότε η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![(-\infty, 0] (-\infty, 0]](/forum/ext/geomar/texintegr/latexrender/pictures/8bb8e3006289394bd593c5b7a4904dd6.png) .
. στο μεταβλητό διάστημα
στο μεταβλητό διάστημα ![[x, 0] [x, 0]](/forum/ext/geomar/texintegr/latexrender/pictures/75f13a252a65c619116a6fb88794269f.png) (
( ) παίρνουμε
) παίρνουμε 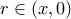 τέτοιο, ώστε
τέτοιο, ώστε 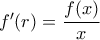 .
.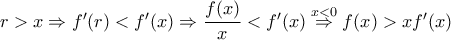 , ή
, ή 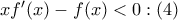 .
.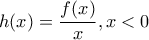 είναι
είναι 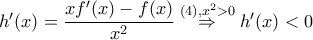 , για κάθε
, για κάθε  , άρα η
, άρα η  είναι γνησίως φθίνουσα.
είναι γνησίως φθίνουσα.  είναι
είναι 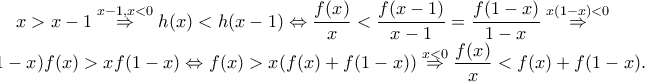
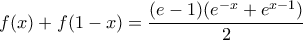 , που δίνει το ζητούμενο.
, που δίνει το ζητούμενο.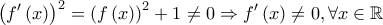 και από τις συνέπειες του Θ. Darboux η
και από τις συνέπειες του Θ. Darboux η 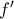 διατηρεί πρόσημο στο
διατηρεί πρόσημο στο  με
με 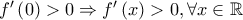 και συνεπώς η
και συνεπώς η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  , άρα αντιστρέφεται. Αφού
, άρα αντιστρέφεται. Αφού 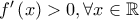 , είναι
, είναι  Θεωρούμε τις συναρτήσεις
Θεωρούμε τις συναρτήσεις 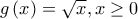 και
και 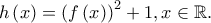 Η
Η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο 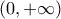 και αφού
και αφού 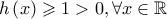 και η
και η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  , έπεται ότι η σύνθεση τους
, έπεται ότι η σύνθεση τους 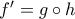 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο 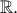 Παραγωγίζοντας την δοθείσα σχέση παίρνουμε
Παραγωγίζοντας την δοθείσα σχέση παίρνουμε 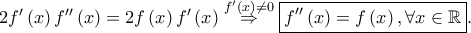
 είναι
είναι 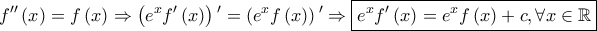 και θέτοντας
και θέτοντας 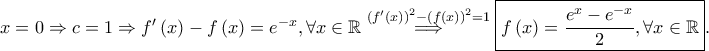
 είναι συνεχής και γνησίως αύξουσα στο
είναι συνεχής και γνησίως αύξουσα στο  , άρα
, άρα 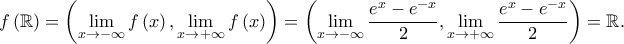
 είναι γνησίως αύξουσα, άρα αντιστρέφεται και
είναι γνησίως αύξουσα, άρα αντιστρέφεται και 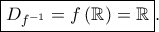 Θέτω
Θέτω 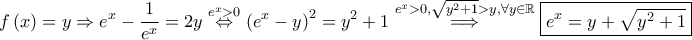
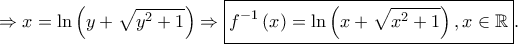
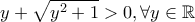 ).
). ![\displaystyle I=\int\limits_{0}^{ 5/4}f^{-1}\left ( x \right )dx=\int\limits_{0}^{5/4}\ln\left ( x+\sqrt{x^{2}+1} \right )dx=\left [ x\ln\left ( x+\sqrt{x^{2}+1} \right ) \right ]_{0}^{5/4}-\int\limits_{0}^{5/4}x\left ( \ln \left ( x+\sqrt{x^{2}+1} \right ) \right ){'}dx \displaystyle I=\int\limits_{0}^{ 5/4}f^{-1}\left ( x \right )dx=\int\limits_{0}^{5/4}\ln\left ( x+\sqrt{x^{2}+1} \right )dx=\left [ x\ln\left ( x+\sqrt{x^{2}+1} \right ) \right ]_{0}^{5/4}-\int\limits_{0}^{5/4}x\left ( \ln \left ( x+\sqrt{x^{2}+1} \right ) \right ){'}dx](/forum/ext/geomar/texintegr/latexrender/pictures/b3200dbe3eba2b68f4ed72eb7756a028.png)
![\displaystyle =\left [ x\ln \left ( x+\sqrt{x^{2}+1} \right ) \right ]_{0}^{5/4}-\int\limits_{0}^{5/4}\frac{x\sqrt{x^{2}+1}+x^{2}}{x\sqrt{x^{2}+1}+x^{2}+1}dx. \displaystyle =\left [ x\ln \left ( x+\sqrt{x^{2}+1} \right ) \right ]_{0}^{5/4}-\int\limits_{0}^{5/4}\frac{x\sqrt{x^{2}+1}+x^{2}}{x\sqrt{x^{2}+1}+x^{2}+1}dx.](/forum/ext/geomar/texintegr/latexrender/pictures/3d01b87f6aa80db5d62a6f3e987c2961.png)
![\displaystyle I=\left [ x\ln \left ( x+\sqrt{x^{2}+1} \right ) \right ]_{0}^{5/4}-\left ( \int\limits_{0}^{5/4}1dx-\int\limits_{0}^{5/4}\frac{1}{x\sqrt{x^{2}+1}+x^{2}+1}dx \right )= \displaystyle I=\left [ x\ln \left ( x+\sqrt{x^{2}+1} \right ) \right ]_{0}^{5/4}-\left ( \int\limits_{0}^{5/4}1dx-\int\limits_{0}^{5/4}\frac{1}{x\sqrt{x^{2}+1}+x^{2}+1}dx \right )=](/forum/ext/geomar/texintegr/latexrender/pictures/9cc623d245ae1892758db0949a632c14.png)
![\displaystyle =\left [ x\ln \left ( x+\sqrt{x^{2}+1} \right ) \right ]_{0}^{5/4}-\frac{5}{4}+\int\limits_{0}^{5/4}\frac{1}{x\sqrt{x^{2}+1}+x^{2}+1}dx. \displaystyle =\left [ x\ln \left ( x+\sqrt{x^{2}+1} \right ) \right ]_{0}^{5/4}-\frac{5}{4}+\int\limits_{0}^{5/4}\frac{1}{x\sqrt{x^{2}+1}+x^{2}+1}dx.](/forum/ext/geomar/texintegr/latexrender/pictures/b2e5eaf0f802ec18de4d0850180347c9.png)
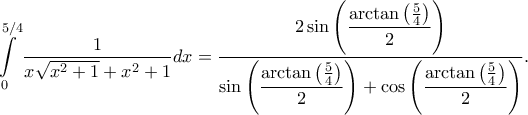
 Η
Η  είναι συνεχής στο
είναι συνεχής στο ![\left [ x-1,x \right ] \left [ x-1,x \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/bed60667a87a40c8645ab1085f00132a.png) και παραγωγίσιμη στο
και παραγωγίσιμη στο 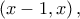 άρα από ΘΜΤ υπάρχει
άρα από ΘΜΤ υπάρχει 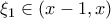 με
με 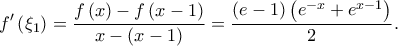
 Ομοίως από ΘΜΤ υπάρχει
Ομοίως από ΘΜΤ υπάρχει 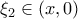 με
με 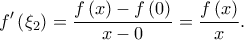
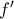 είναι συνεχής στο
είναι συνεχής στο ![\left ( -\infty,0 \right ] \left ( -\infty,0 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/f9ba2e4f06af7d5f93b7cdd6a043ed41.png) και παραγωγίσιμη στο
και παραγωγίσιμη στο 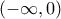 με
με 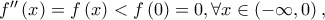 αφού η
αφού η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  , άρα η
, άρα η 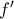 είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![\left ( -\infty,0 \right ] \left ( -\infty,0 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/f9ba2e4f06af7d5f93b7cdd6a043ed41.png) και αφού
και αφού 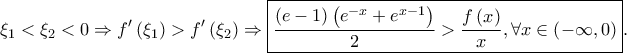
Αφού ηthepigod762 έγραψε: ↑Τρί Ιαν 02, 2024 10:32 pm
Άρα η f είναι 1-1, οπότε αντιστρέφεται.
Επειδή η f είναι 1-1 και συνεχής στο, είναι γνησίως μονότονη στο
.
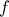 είναι γνησίως μονότονη και
είναι γνησίως μονότονη και 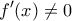 τότε
τότε 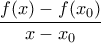 θετικό για κάθε
θετικό για κάθε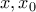 , ή αρνητικό για κάθε
, ή αρνητικό για κάθε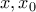 με
με 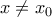
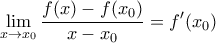 θα είναι θετικό για κάθε
θα είναι θετικό για κάθε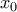 ή αρνητικό για κάθε
ή αρνητικό για κάθε 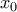 .
. 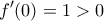 και έτσι θα πρέπει
και έτσι θα πρέπει 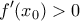 για κάθε
για κάθε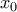 .
.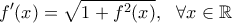 και συνεπώς η
και συνεπώς η  θα είναι παραγωγίσιμη - πράξεις παραγωγίσιμων συναρτήσεων.
θα είναι παραγωγίσιμη - πράξεις παραγωγίσιμων συναρτήσεων.

 μια αρχική της
μια αρχική της  στο
στο  με
με 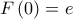 και
και 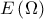 το εμβαδόν του χωρίου
το εμβαδόν του χωρίου 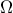 που περικλείεται από την γραφική παράσταση της συνάρτησης
που περικλείεται από την γραφική παράσταση της συνάρτησης  με
με 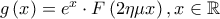 και την εφαπτομένη της
και την εφαπτομένη της  στο σημείο της με τετμημένη
στο σημείο της με τετμημένη 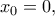 ανάμεσα στις ευθείες
ανάμεσα στις ευθείες  και
και 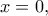 να αποδείξετε ότι:
να αποδείξετε ότι: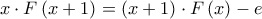 έχει μοναδική ρίζα στο
έχει μοναδική ρίζα στο 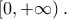
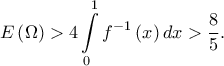
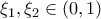 με
με 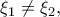 τέτοια ώστε
τέτοια ώστε 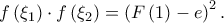
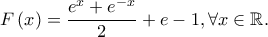
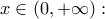
 Η
Η  είναι συνεχής στο
είναι συνεχής στο ![\left [ 0,x \right ] \left [ 0,x \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/38a2c48f3b251133cdf16a1d1af77d74.png) και παραγωγίσιμη στο
και παραγωγίσιμη στο 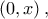 άρα από ΘΜΤ υπάρχει
άρα από ΘΜΤ υπάρχει 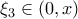 με
με 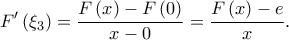
 Η
Η  είναι συνεχής στο
είναι συνεχής στο ![\left [ x,x+1 \right ] \left [ x,x+1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/630e8eb2f9a5f4b1efd9e84251cbf148.png) και παραγωγίσιμη στο
και παραγωγίσιμη στο 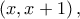 άρα από ΘΜΤ υπάρχει
άρα από ΘΜΤ υπάρχει 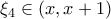 με
με 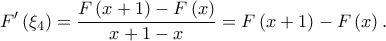
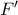 είναι παραγωγίσιιμη με
είναι παραγωγίσιιμη με 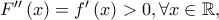 άρα η
άρα η 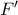 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  και αφού
και αφού 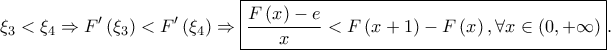 Επομένως:
Επομένως: 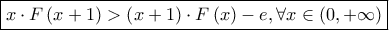 και συνεπώς η εξίσωση έχει μοναδική λύση στο
και συνεπώς η εξίσωση έχει μοναδική λύση στο 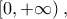 την
την  που επαληθεύει την δοθείσα.
που επαληθεύει την δοθείσα.  είναι συνεχής στο
είναι συνεχής στο ![\left ( -\infty,0 \right ] \left ( -\infty,0 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/f9ba2e4f06af7d5f93b7cdd6a043ed41.png) και παραγωγίσιμη στο
και παραγωγίσιμη στο 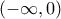 με
με 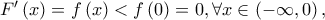 αφού η
αφού η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  άρα η
άρα η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![\left ( -\infty,0 \right ]. \left ( -\infty,0 \right ].](/forum/ext/geomar/texintegr/latexrender/pictures/2b1137a7d4516204f6c733774a3982e3.png) Αφού
Αφού 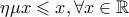 με την ισότητα μόνο για
με την ισότητα μόνο για 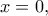 άρα
άρα ![2\eta \mu x\leqslant x,\forall x\in \left ( -\infty,0 \right ], 2\eta \mu x\leqslant x,\forall x\in \left ( -\infty,0 \right ],](/forum/ext/geomar/texintegr/latexrender/pictures/5340b248841eee6c05c48c3dffe99c0e.png) με την ισότητα μόνο για
με την ισότητα μόνο για  και αφού η
και αφού η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![\left ( -\infty,0 \right ], \left ( -\infty,0 \right ],](/forum/ext/geomar/texintegr/latexrender/pictures/48568e90e689498f4445cd6d42d5af37.png) έχουμε
έχουμε ![F\left ( 2\eta \mu x \right )\geqslant F\left ( x \right ),\forall x\in \left ( -\infty,0 \right ] F\left ( 2\eta \mu x \right )\geqslant F\left ( x \right ),\forall x\in \left ( -\infty,0 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/f109f8c5b4288c3ddeef3fcbda6a80b9.png) με την ισότητα μόνο για
με την ισότητα μόνο για 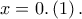
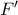 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  , άρα η
, άρα η  είναι κυρτή στο
είναι κυρτή στο  και αφού η εξίσωση εφαπτομένης της
και αφού η εξίσωση εφαπτομένης της  στο σημείο της
στο σημείο της 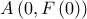 είναι
είναι 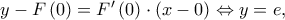 επομένως
επομένως 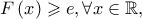 με την ισότητα μόνο για
με την ισότητα μόνο για 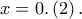 Από τις σχέσεις
Από τις σχέσεις 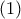 και
και  παίρνουμε
παίρνουμε ![F\left ( 2\eta \mu x \right )\geqslant e,\forall x\in \left ( -\infty,0 \right ], F\left ( 2\eta \mu x \right )\geqslant e,\forall x\in \left ( -\infty,0 \right ],](/forum/ext/geomar/texintegr/latexrender/pictures/a78f612c5a5688b73cf9eefe8b0d3a4b.png) με την ισότητα μόνο για
με την ισότητα μόνο για  και πολλαπλασιάζοντας με
και πολλαπλασιάζοντας με 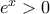 έχουμε
έχουμε ![e^{x}\cdot F\left ( 2\eta \mu x \right )\geqslant e^{x+1},\forall x\in \left ( -\infty,0 \right ], e^{x}\cdot F\left ( 2\eta \mu x \right )\geqslant e^{x+1},\forall x\in \left ( -\infty,0 \right ],](/forum/ext/geomar/texintegr/latexrender/pictures/0d279bc4dcb300fb3150bef3901096a8.png) με την ισότητα μόνο για
με την ισότητα μόνο για  Επομένως:
Επομένως: ![\displaystyle \boxed{e^{x}\cdot F\left ( 2\eta \mu x \right )-x\geqslant e^{x+1}-x,\forall x\in \left ( -\infty,0 \right ]}, \displaystyle \boxed{e^{x}\cdot F\left ( 2\eta \mu x \right )-x\geqslant e^{x+1}-x,\forall x\in \left ( -\infty,0 \right ]},](/forum/ext/geomar/texintegr/latexrender/pictures/9142fbf4dea6cd617019027978133d04.png) με την ισότητα μόνο για
με την ισότητα μόνο για 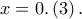 Η εξίσωση εφαπτομένης της
Η εξίσωση εφαπτομένης της  στο σημείο της με τετμημένη
στο σημείο της με τετμημένη 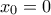 είναι
είναι 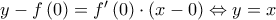 και άρα το ζητούμενο εμβαδόν είναι
και άρα το ζητούμενο εμβαδόν είναι 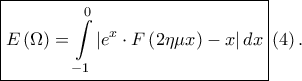 Από την σχέση
Από την σχέση  λαμβάνουμε
λαμβάνουμε ![\boxed{e^{x}\cdot F\left ( 2\eta \mu x \right )-x\geqslant e^{x+1}-x\geqslant 2> 0,\forall x\in \left ( -\infty,0 \right ]}\overset{\left ( 4 \right )}\Rightarrow \boxed{E\left ( \Omega \right )=\int\limits_{-1}^{0} (e^{x}\cdot F\left ( 2\eta \mu x \right)-x) dx}\left ( 5 \right ). \boxed{e^{x}\cdot F\left ( 2\eta \mu x \right )-x\geqslant e^{x+1}-x\geqslant 2> 0,\forall x\in \left ( -\infty,0 \right ]}\overset{\left ( 4 \right )}\Rightarrow \boxed{E\left ( \Omega \right )=\int\limits_{-1}^{0} (e^{x}\cdot F\left ( 2\eta \mu x \right)-x) dx}\left ( 5 \right ).](/forum/ext/geomar/texintegr/latexrender/pictures/f461ac7dd29a535f75ee6353dad693de.png) Επίσης, από την σχέση
Επίσης, από την σχέση  έχουμε
έχουμε ![e^{x}\cdot F\left ( 2\eta \mu x \right )-x\geqslant e^{x+1}-x,\forall x\in \left ( -\infty,0 \right ], e^{x}\cdot F\left ( 2\eta \mu x \right )-x\geqslant e^{x+1}-x,\forall x\in \left ( -\infty,0 \right ],](/forum/ext/geomar/texintegr/latexrender/pictures/d6adb7c253c291fbc56ec47341d48756.png) με την ισότητα μόνο για
με την ισότητα μόνο για  Επομένως :
Επομένως : ![\displaystyle \boxed{E\left ( \Omega \right )\overset{\left ( 5 \right )}=\int\limits_{-1}^{0}\left ( e^{x}\cdot F\left ( 2\eta \mu x \right )-x \right )dx> \int\limits_{-1}^{0}\left ( e^{x+1}-x \right )dx=\left [ e^{x+1}-\frac{x^{2}}{2} \right ]_{-1}^{0}=e-\frac{1}{2}> 2}\left ( 6 \right ). \displaystyle \boxed{E\left ( \Omega \right )\overset{\left ( 5 \right )}=\int\limits_{-1}^{0}\left ( e^{x}\cdot F\left ( 2\eta \mu x \right )-x \right )dx> \int\limits_{-1}^{0}\left ( e^{x+1}-x \right )dx=\left [ e^{x+1}-\frac{x^{2}}{2} \right ]_{-1}^{0}=e-\frac{1}{2}> 2}\left ( 6 \right ).](/forum/ext/geomar/texintegr/latexrender/pictures/09be45841b6160930923a0b0145e23da.png)
 Κάνουμε την αντικατάσταση
Κάνουμε την αντικατάσταση 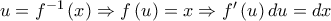 και τα άκρα ολοκλήρωσης γίνονται
και τα άκρα ολοκλήρωσης γίνονται 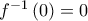 και
και 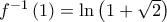 και έχουμε
και έχουμε ![\displaystyle \boxed{\int\limits_{0}^{1}f^{-1}\left ( x \right )dx=\int\limits_{0}^{\ln\left ( 1+\sqrt{2} \right )}uf{'}\left ( u \right )du=\left [ uf\left ( u \right ) \right ]_{0}^{\ln\left ( 1+\sqrt{2} \right )}-\int\limits_{0}^{\ln\left ( 1+\sqrt{2} \right )}f\left ( u \right )du}\left ( 7 \right ). \displaystyle \boxed{\int\limits_{0}^{1}f^{-1}\left ( x \right )dx=\int\limits_{0}^{\ln\left ( 1+\sqrt{2} \right )}uf{'}\left ( u \right )du=\left [ uf\left ( u \right ) \right ]_{0}^{\ln\left ( 1+\sqrt{2} \right )}-\int\limits_{0}^{\ln\left ( 1+\sqrt{2} \right )}f\left ( u \right )du}\left ( 7 \right ).](/forum/ext/geomar/texintegr/latexrender/pictures/78f3a77543ea9f98cf02849f7ad0ec5a.png) Είναι
Είναι ![\displaystyle \int\limits _{0}^{\ln\left ( 1+\sqrt{2} \right )}f\left ( u \right )du=\left [ \frac{e^{u}+e^{-u}}{2} \right ]_{0}^{\ln\left ( 1+\sqrt{2} \right )}=\frac{\displaystyle 1+\sqrt{2}+\frac{1}{1+\sqrt{2}}}{2}-1=\sqrt{2}-1 \overset{\left ( 7 \right )}\Rightarrow \boxed{\int\limits_{0}^{1}f^{-1}\left ( x \right )dx=\ln\left ( 1+\sqrt{2} \right )-\sqrt{2}+1}\left ( 8 \right ). \displaystyle \int\limits _{0}^{\ln\left ( 1+\sqrt{2} \right )}f\left ( u \right )du=\left [ \frac{e^{u}+e^{-u}}{2} \right ]_{0}^{\ln\left ( 1+\sqrt{2} \right )}=\frac{\displaystyle 1+\sqrt{2}+\frac{1}{1+\sqrt{2}}}{2}-1=\sqrt{2}-1 \overset{\left ( 7 \right )}\Rightarrow \boxed{\int\limits_{0}^{1}f^{-1}\left ( x \right )dx=\ln\left ( 1+\sqrt{2} \right )-\sqrt{2}+1}\left ( 8 \right ).](/forum/ext/geomar/texintegr/latexrender/pictures/9e91a403a619dc27e50ba9a1d2e1ebae.png)
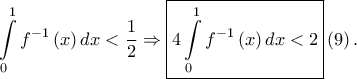 Από τις σχέσεις
Από τις σχέσεις 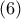 και
και 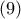 παίρνουμε
παίρνουμε 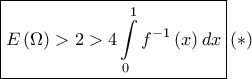 και αφού
και αφού 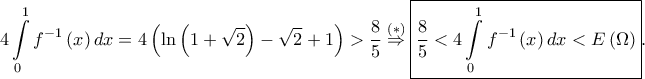
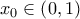 που θα διαλέξουμε στη συνέχεια. Από ΘΜΤ στα διαστήματα
που θα διαλέξουμε στη συνέχεια. Από ΘΜΤ στα διαστήματα ![\left [ 0,x_{0} \right ],\left [ x_{0},1 \right ] \left [ 0,x_{0} \right ],\left [ x_{0},1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/6ad8a37607d69934a270e521086c4133.png) (ικανοποιούνται οι προύποθέσεις) υπάρχουν
(ικανοποιούνται οι προύποθέσεις) υπάρχουν 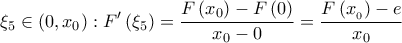 και
και 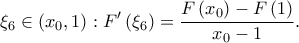 Επομένως
Επομένως 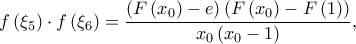 πρέπει λοιπόν ισοδύναμα να υπάρχει
πρέπει λοιπόν ισοδύναμα να υπάρχει 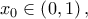 τέτοιο ώστε
τέτοιο ώστε 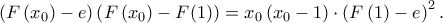 Θεωρούμε την συνάρτηση
Θεωρούμε την συνάρτηση ![p\left ( x \right )=\left ( F\left ( x \right )-e \right )\left ( F\left ( x \right ) -F\left ( 1 \right )\right )-x\left ( x-1 \right )\left ( F\left ( 1 \right )-e \right )^{2},x\in \left [ 0,1 \right ]. p\left ( x \right )=\left ( F\left ( x \right )-e \right )\left ( F\left ( x \right ) -F\left ( 1 \right )\right )-x\left ( x-1 \right )\left ( F\left ( 1 \right )-e \right )^{2},x\in \left [ 0,1 \right ].](/forum/ext/geomar/texintegr/latexrender/pictures/98c5df53744c32b7cefcfce60fcaee5c.png) Είναι
Είναι 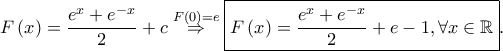 Επομένως
Επομένως ![\displaystyle p\left ( x \right )=\left ( \frac{e^{x}+e^{-x}}{2}-1 \right )\left ( \frac{e^{x}+e^{-x}}{2}-\frac{e^{2}+1}{2e} \right )-\left ( \frac{e^{2}+1}{2e}-e \right )^{2}\cdot x\left ( x-1 \right ),x\in \left [ 0,1 \right ]. \displaystyle p\left ( x \right )=\left ( \frac{e^{x}+e^{-x}}{2}-1 \right )\left ( \frac{e^{x}+e^{-x}}{2}-\frac{e^{2}+1}{2e} \right )-\left ( \frac{e^{2}+1}{2e}-e \right )^{2}\cdot x\left ( x-1 \right ),x\in \left [ 0,1 \right ].](/forum/ext/geomar/texintegr/latexrender/pictures/178179e65d2f0b10a97d6d7f6f70481d.png) Με μελέτη δείχνουμε ότι υπάρχει
Με μελέτη δείχνουμε ότι υπάρχει 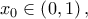 τέτοιο ώστε
τέτοιο ώστε 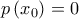 και η απόδειξη ολοκληρώνεται. Είναι στην ουσία το όμορφο και εύκολο ερώτημα από εδώ https://www.mathematica.gr/forum/viewto ... B7#p361140.
και η απόδειξη ολοκληρώνεται. Είναι στην ουσία το όμορφο και εύκολο ερώτημα από εδώ https://www.mathematica.gr/forum/viewto ... B7#p361140.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες