 δεν υπάρχει.
δεν υπάρχει.Σημείωση #1:
Το ζητούμενο μπορεί αποδειχθεί πολύ εύκολα αν:
1) χρησιμοποιηθεί ο ορισμός του ορίου με

2) χρησιμοποιηθούν ακολουθίες πραγματικών αριθμών και ο ακολουθιακός ορισμός του ορίου
3) είναι κανείς διατεθειμένος να αρκεστεί στην εποπτεία που προσφέρει μια γραφική παράσταση.
Επειδή τα 1),2) δεν αφορούν την ύλη των πανελληνίων εξετάσεων, δεν έχουν θέση στο πλαίσιο της παρούσας ανάρτησης. Σε ό,τι αφορά το 3), ενώ οι γραφικές παραστάσεις είναι χρήσιμες κατά την επίλυση προβλημάτων, στα μαθηματικά αυτό που μας ενδιαφέρει τελικά είναι οι τυπικές αποδείξεις. Μια γραφική παράσταση είναι ισόκυρη με μια τυπική απόδειξη μόνο όταν υπάρχει βεβαιότητα ότι όντως κωδικοποιεί επαρκώς και μπορεί να οδηγήσει με προφανή τρόπο (αν και ενδεχομένως με ανείπωτο μόχθο) στη διατύπωση μιας τυπικής απόδειξης. Όταν κάποιος διαθέτει τα εργαλεία στα 1),2) μπορεί να ισχυριστεί ότι μια γραφική παράσταση της
 κωδικοποιεί μια απόδειξη. Επειδή όμως έχουμε τους περιορισμούς των πανελληνίων εξετάσεων δεν είναι προφανές πως ακριβώς μια γραφική παράσταση κωδικοποιεί μια εντός ύλης, "νόμιμη", τυπική απόδειξη.
κωδικοποιεί μια απόδειξη. Επειδή όμως έχουμε τους περιορισμούς των πανελληνίων εξετάσεων δεν είναι προφανές πως ακριβώς μια γραφική παράσταση κωδικοποιεί μια εντός ύλης, "νόμιμη", τυπική απόδειξη.Για να περάσουμε στο δια ταύτα, μια αποδεκτή λύση για την παρούσα θα πρέπει να συμμορφώνεται με το ακόλουθο πρότυπο:
#1. Να χρησιμοποιεί αποκλειστικά θεωρήματα και ιδιότητες που είναι διαθέσιμα σε έναν υποψήφιο των πανελληνίων εξετάσεων.
#2. Να μην επικαλείται/βασίζεται σε εποπτεία/γεωμετρικές ερμηνείες/γραφικές παραστάσεις.
Σημείωση #2: Ενδεικτικά η άσκηση μπορεί να λυθεί με την ύλη που είναι διαθέσιμη μέχρι και την παράγραφο 1.6 του σχολικού βιβλίου "Μη πεπερασμένο όριο στο
 ".
".
 . Έστω ότι υπήρχε και ήταν
. Έστω ότι υπήρχε και ήταν  . Τότε
. Τότε  , άρα
, άρα  . Επίσης
. Επίσης 
 . Άτοπο.
. Άτοπο.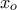 "
" έχει λύσεις σε οποιοδήποτε διάστημα
έχει λύσεις σε οποιοδήποτε διάστημα  με
με  . Πράγματι, για κάθε θετικό ακέραιο
. Πράγματι, για κάθε θετικό ακέραιο  με
με  ο
ο  είναι μια λύση στο
είναι μια λύση στο  . Διακρίνουμε τις περιπτώσεις:
. Διακρίνουμε τις περιπτώσεις: ή
ή  και
και 
 κοντά στο
κοντά στο 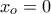 οπότε θα υπάρχει
οπότε θα υπάρχει  έχει λύσεις στο
έχει λύσεις στο  ή
ή 
 κοντά στο
κοντά στο  έχει λύσεις στο
έχει λύσεις στο 
 οπότε θα υπάρχει
οπότε θα υπάρχει  στο
στο