1. Να βρειτε όλα τα μη μηδενικά πολυώνυμα
 ώστε
ώστε
2. Να βρείτε όλα τα μη μηδενικά πολυώνυμα
 ώστε
ώστε 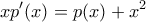
3. Να βρειτε όλα τα μη μηδενικά πολυώνυμα
 ώστε το
ώστε το  να είναι παράγοντας του
να είναι παράγοντας του
4.Αν οι ρίζες του πολυωνύμου p είναι όλες απλές και πραγματικές να δείξετε
a)
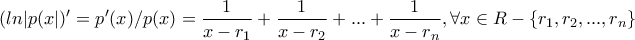 και
καιb) το πολυώνυμο
 δεν έχει πραγματικές ρίζες
δεν έχει πραγματικές ρίζες5. Να δείξετε ότι δεν υπάρχουν πολυώνυμα
 ώστε για κάθε
ώστε για κάθε  να ισχύει
να ισχύει ( ασχοληθείτε με όρια και βαθμούς. Πιθανόν και με παραγωγίσεις)
( ασχοληθείτε με όρια και βαθμούς. Πιθανόν και με παραγωγίσεις)6. .Αν βαθ(p)=άρτιος τότε το p έχει ολικό ακρότατο
7.Αν οι ρίζες του πολυωνύμου
 είναι όλες απλές και πραγματικές να δείξετε ότι οι ρίζες του
είναι όλες απλές και πραγματικές να δείξετε ότι οι ρίζες του  είναι πραγματκές για οποιαδποτε πραγματική τιμή του
είναι πραγματκές για οποιαδποτε πραγματική τιμή του  Εδώ θα βοηθούσαν λίγα πράγματα για μιγαδικούς
Εδώ θα βοηθούσαν λίγα πράγματα για μιγαδικούς
 με
με  καθώς αν
καθώς αν  το πρώτο μέλος είναι το μηδενικό πολυώνυμο
το πρώτο μέλος είναι το μηδενικό πολυώνυμο και το
και το  έχει βαθμό
έχει βαθμό  .
. .
. με
με  . Τότε
. Τότε  και έτσι η ισότητα γίνεται :
και έτσι η ισότητα γίνεται :
 από την (1) έχουμε
από την (1) έχουμε  και με αντικατάσταση στη (2) :
και με αντικατάσταση στη (2) :  και έτσι
και έτσι
 άρα
άρα 

 δηλαδή
δηλαδή 

 ως πολυωνυμική, άρα με παραγώγιση της δοσμένης έχουμε
ως πολυωνυμική, άρα με παραγώγιση της δοσμένης έχουμε . Η σχέση ισχύει για κάθε
. Η σχέση ισχύει για κάθε  άρα έχουμε
άρα έχουμε με
με  και με αντικατάσταση
και με αντικατάσταση  .
. .
. και
και 
 ώστε για κάθε
ώστε για κάθε  να είναι
να είναι  .
. θα έχουμε ότι
θα έχουμε ότι  και
και  .
.

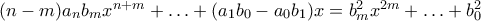
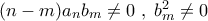 οπότε
οπότε  , άτοπο.
, άτοπο.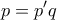 με
με  πολυώνυμο προφανώς 1ου βαθμού (
πολυώνυμο προφανώς 1ου βαθμού ( ) και απο την εξίσωση μεγιστοβαθμίων και σταθερών
) και απο την εξίσωση μεγιστοβαθμίων και σταθερών  άρα
άρα παραγωγίζουμε
παραγωγίζουμε  ξανά
ξανά  ξανά
ξανά 



 άρα
άρα  για
για  εφαρμόζοντας η φορές τον κανόνα DLH και αφού
εφαρμόζοντας η φορές τον κανόνα DLH και αφού  βρισκουμε
βρισκουμε  οπότε
οπότε 
 αν το
αν το  θα είχε και αυτο ριζα , όχι την
θα είχε και αυτο ριζα , όχι την  , λόγω Θ.Ρολλ. Από το πεπερασμένο πληθος ριζών του
, λόγω Θ.Ρολλ. Από το πεπερασμένο πληθος ριζών του  η πλησιέστερη προς την
η πλησιέστερη προς την  ρίζα του
ρίζα του  και από τους μεγιστοβάθμιους
και από τους μεγιστοβάθμιους 
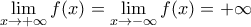
 υπάρχει λοιπόν
υπάρχει λοιπόν 
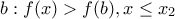
![\displaystyle{ [x_2,x_1]} \displaystyle{ [x_2,x_1]}](/forum/ext/geomar/texintegr/latexrender/pictures/b5822e5dae7dbfc5a93ea42959ecc6d9.png) η
η  έχει ως συνεχής έχει ΜΙΝ το
έχει ως συνεχής έχει ΜΙΝ το 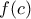
 Tότε
Tότε  με
με  αρκεί
αρκεί 
 (απόδειξη χωρίς παραγώγους) όπου
(απόδειξη χωρίς παραγώγους) όπου  το
το  και διαιρούμε με
και διαιρούμε με  από το κριτήριο παρεμβολής έχουμε το ζητούμενο
από το κριτήριο παρεμβολής έχουμε το ζητούμενο ,
,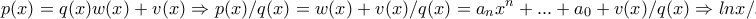 με
με 

 άτοπο
άτοπο  από Bernoulli
από Bernoulli  παίρνοντας όρια καταλήγουμε στην
παίρνοντας όρια καταλήγουμε στην  όπου
όπου  προκύπτει
προκύπτει  τελικά όπου
τελικά όπου 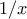 και φτάσαμε στο ζητούμενο
και φτάσαμε στο ζητούμενο