 για τους οποίους ισχύει
για τους οποίους ισχύει  τους οποίους να βρείτε.
τους οποίους να βρείτε.Συντονιστής: KAKABASBASILEIOS
 για τους οποίους ισχύει
για τους οποίους ισχύει  τους οποίους να βρείτε.
τους οποίους να βρείτε.
 . Ακόμη
. Ακόμη 
 . Άρα:
. Άρα: 
 με πρώτη παραγωγο:
με πρώτη παραγωγο: 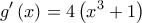
 από πίνακα μονοτονιας πάλι έχουμε ολικό ελαχιστο στο
από πίνακα μονοτονιας πάλι έχουμε ολικό ελαχιστο στο  άρα
άρα 
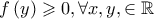 . Για να ισχύει θα πρέπει
. Για να ισχύει θα πρέπει 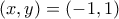

 , βρίσκουμε ότι έχει ολικό ελάχιστο το 10, το οποίο παρουσιάζει στη θέση 1
, βρίσκουμε ότι έχει ολικό ελάχιστο το 10, το οποίο παρουσιάζει στη θέση 1 , βρίσκουμε ότι έχει ολικό μέγιστο το 10, το οποίο παρουσιάζει στη θέση -1
, βρίσκουμε ότι έχει ολικό μέγιστο το 10, το οποίο παρουσιάζει στη θέση -1
Ακριβώς αυτόν το τρόπο είχα και εγω στο μυαλό μου. Η f έχει σύνολο τιμών τοs.kap έγραψε:Παναγιώτη, πολύ έξυπνη άσκηση
Η δοθείσα εξίσωση γράφεται
Μελετώντας με τη βοήθεια της πρώτης παραγώγου τη συνάρτηση, βρίσκουμε ότι έχει ολικό ελάχιστο το 10, το οποίο παρουσιάζει στη θέση 1
Μελετώντας με τη βοήθεια της πρώτης παραγώγου τη συνάρτηση, βρίσκουμε ότι έχει ολικό μέγιστο το 10, το οποίο παρουσιάζει στη θέση -1
Άρα για να αληθεύει η εξίσωση πρέπει και αρκεί
Φιλικά
Είδα ότι με πρόλαβε ο Κωστάκης. Πολύ χαίρομαι
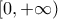 και η g το
και η g το ![[-10,10] [-10,10]](/forum/ext/geomar/texintegr/latexrender/pictures/501dda82f274782fb69dd20dbdef7fc2.png) κ.ο.κ. Ευχαριστώ
κ.ο.κ. ΕυχαριστώΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες