 με
με  και
και  , για κάθε
, για κάθε  .
.Μπ.
Συντονιστής: KAKABASBASILEIOS
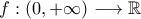 μια παραγωγίσιμη συνάρτηση με
μια παραγωγίσιμη συνάρτηση με  και τέτοια,
και τέτοια, για κάθε
για κάθε  .
. έχουμε
έχουμε  ή ισοδύναμα
ή ισοδύναμα για κάθε
για κάθε  .
. ,
, .
. έχουμε :
έχουμε :![\displaystyle{\begin{aligned} f^\prime(x)-g^\prime(x)\,f(x)=0&\iff e^{-g(x)}\,f^\prime(x)-e^{-g(x)}\,g^\prime(x)\,f(x)=0\\&\iff \left[e^{-g(x)}\,f(x)\right]'=0\\&\iff \left(\exists\,c\in\mathbb{R}\right)\,\left(\forall\,x>0\right): e^{-g(x)}\,f(x)=c\end{aligned}} \displaystyle{\begin{aligned} f^\prime(x)-g^\prime(x)\,f(x)=0&\iff e^{-g(x)}\,f^\prime(x)-e^{-g(x)}\,g^\prime(x)\,f(x)=0\\&\iff \left[e^{-g(x)}\,f(x)\right]'=0\\&\iff \left(\exists\,c\in\mathbb{R}\right)\,\left(\forall\,x>0\right): e^{-g(x)}\,f(x)=c\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/75ba43da3eb615e29ed14e3d6b7cf0d4.png)
 λαμβάνουμε :
λαμβάνουμε : 
 , όπου για
, όπου για  είναι :
είναι :![\displaystyle{\begin{aligned}g(x)&=\int_{1}^{x}\dfrac{2014}{t+t^{2015}}\,\mathrm{d}t\\&=\int_{1}^{x}\dfrac{2014\,t^{2013}}{t^{2014}\,\left(1+t^{2014}\right)}\,\mathrm{d}t\\&=\int_{1}^{x}\dfrac{\left(1+t^{2014}\right)-t^{2014}}{t^{2014}\,\left(1+t^{2014}\right)}\,\mathrm{d}\,\left(t^{2014}\right)\\&=\int_{1}^{x}\left[\dfrac{1}{t^{2014}}-\dfrac{1}{1+t^{2014}}\right]\,\mathrm{d}\,\left(t^{2014}\right)\\&=\left[\ln\,t^{2014}-\ln\,(1+t^{2014})\right]_{1}^{x}\\&=\ln\,\dfrac{x^{2014}}{1+x^{2014}}+\ln\,2\\&=\ln\,\dfrac{2\,x^{2014}}{1+x^{2014}}\end{aligned}} \displaystyle{\begin{aligned}g(x)&=\int_{1}^{x}\dfrac{2014}{t+t^{2015}}\,\mathrm{d}t\\&=\int_{1}^{x}\dfrac{2014\,t^{2013}}{t^{2014}\,\left(1+t^{2014}\right)}\,\mathrm{d}t\\&=\int_{1}^{x}\dfrac{\left(1+t^{2014}\right)-t^{2014}}{t^{2014}\,\left(1+t^{2014}\right)}\,\mathrm{d}\,\left(t^{2014}\right)\\&=\int_{1}^{x}\left[\dfrac{1}{t^{2014}}-\dfrac{1}{1+t^{2014}}\right]\,\mathrm{d}\,\left(t^{2014}\right)\\&=\left[\ln\,t^{2014}-\ln\,(1+t^{2014})\right]_{1}^{x}\\&=\ln\,\dfrac{x^{2014}}{1+x^{2014}}+\ln\,2\\&=\ln\,\dfrac{2\,x^{2014}}{1+x^{2014}}\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/2786e22620c2bb303bc291c02cb51b6c.png)

 με
με 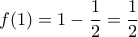 και παράγωγο :
και παράγωγο : , άρα :
, άρα :
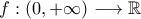 με τύπο
με τύπο 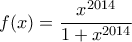
ΕίναιΜπάμπης Στεργίου έγραψε:Να βρεθεί η παραγωγίσιμη συνάρτησημε
και
, για κάθε
.
Μπ.

 ,τότε
,τότε 


 ,ικανοποιεί τις αρχικές συνθήκες.
,ικανοποιεί τις αρχικές συνθήκες. και τα δύο μέλη, τότε
και τα δύο μέλη, τότε





 βρίσκουμε
βρίσκουμε 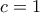 , άρα
, άρα 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες