Καλημέρα,
Η γεωμετρική ιδέα για το ερώτημα (1) ήταν να επινοήσουμε μια συνάρτηση που ναι μεν να τείνει στο άπειρο στο ένα άκρο του διαστήματος αλλά αυτή η αύξηση να είναι όχι με "ομοιόμορφο" τρόπο αλλά με κάποιου είδους ταλάντωση. Και μάλιστα ο "ρυθμός μεταβολής" της περιόδου αυτής της ταλάντωσης καθώς θα τείνουμε στο άκρο που απειρίζεται, να είναι μεγαλύτερος από το "ρυθμό" με τον οποίο αυξάνεται η συνάρτηση.
Παρόμοια ιδέα μπορεί να εφαρμοστεί και για το ερώτημα (2) .Υυποψιάζομαι οτι αυτό κάνει η ολοκλήρωση που ανέφερε ο κ.Δημήτρης παραπάνω.
Ας θεωρήσουμε για παράδειγμα την συνάρτηση

στο διάστημα
![[[0,1] [[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/e0e7f109a74b3ec224ffeb94b34335f5.png)
(την γνησίως φθίνουσα ημιπερίοδο της). Η συνάρτηση σε αυτό το διάστημα είναι γνησίως φθίνουσα αλλά δεν είναι κυρτή.
Θα προσπαθήσουμε τώρα να συγκολλήσουμε τέτοια κομμάτια συναρτήσεων το ένα δίπλα στο άλλο για να δημιουργήσουμε την συνάτηση ανιπαράδειγμα που επιδιώκουμε. Ξεκινώντας από ένα σημείο έστω το

διαμερίζουμε το διάστημα
![[0,c] [0,c]](/forum/ext/geomar/texintegr/latexrender/pictures/0b77a0c57e4d83ea934d4ef032e10c08.png)
σε διαστήματα

μήκους

. Δηλαδή το πρώτο διάστημα θα είναι
![d_{1}=[c-1,c] d_{1}=[c-1,c]](/forum/ext/geomar/texintegr/latexrender/pictures/880c814f9566d398d3c4b06c2ff5aef3.png)
μήκους 1, το δέυτερο
![d_{2}= [c -1 -\dfrac{1}{2^2},c-1] d_{2}= [c -1 -\dfrac{1}{2^2},c-1]](/forum/ext/geomar/texintegr/latexrender/pictures/8a6a6af52f2d104f140a8ca66c38bced.png)
μήκους
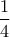
κτλ.
Σε καθένα από αυτά τα διαστήματα θεωρούμε τις συναρτήσεις

και κρατάμε μόνο το γνησίως φθίνουσο κομμάτι μιας ημιπεριόδου τους. Η συνάρτηση που σχηματίζεται από τις συγκολλήσεις συναρτήσεων της παραπάνω μορφής είναι γνησίως φθίνουσα.
Εφόσον η σειρά

συγκλίνει τα διαστήματα θα τείνουν όλο και πιο κοντά στο μηδέν. Από την άλλη επειδή η σειρά
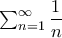
αποκλείνει η συνάρτηση καθώς θα τείνουμε στο μηδέν θα απειρίζεται.
Τώρα οποιοδήποτε

και να διαλέξουμε θα βρεθεί ένα αρκόυντως μεγάλο

για το οποίο το διάστημα

θα βρίσκεται στο

, στο οποίο η συνάρτηση δεν είναι κυρτή.
Μένει βέβαια να δείξουμε ότι οι συγκολλήσεις είναι "λείες" δηλαδή ότι υπάρχει η παράγωγος στα σημεία αυτά και είναι ίση με μηδέν

.
 ορισμένη και παραγωγίσιμη σε διάστημα
ορισμένη και παραγωγίσιμη σε διάστημα  ώστε
ώστε  τότε υπάρχει
τότε υπάρχει  ώστε
ώστε  κυρτή στο
κυρτή στο ![(\alpha ,\,\beta ] (\alpha ,\,\beta ]](/forum/ext/geomar/texintegr/latexrender/pictures/7d95a7f607c01c6a0efbf4a6f83d2c00.png) .
. ορισμένη και παραγωγίσιμη σε διάστημα
ορισμένη και παραγωγίσιμη σε διάστημα  ώστε
ώστε  και γνήσια φθίνουσα στο
και γνήσια φθίνουσα στο  τότε υπάρχει
τότε υπάρχει  ώστε
ώστε  κυρτή στο
κυρτή στο ![(\alpha ,\,\beta ] (\alpha ,\,\beta ]](/forum/ext/geomar/texintegr/latexrender/pictures/7d95a7f607c01c6a0efbf4a6f83d2c00.png) .
.
 και ως "διαμόρφωσή" της την συνάρτηση
και ως "διαμόρφωσή" της την συνάρτηση 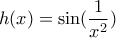 . Τότε η συνάρτηση
. Τότε η συνάρτηση  είναι ένα αντιπαράδειγμα (κατάλληλη μετατόπισή της κατά
είναι ένα αντιπαράδειγμα (κατάλληλη μετατόπισή της κατά  ).
). είναι συν άπειρο.
είναι συν άπειρο.
 στο
στο  θα αλλάζει πρόσημο στο διάστημα
θα αλλάζει πρόσημο στο διάστημα  αφού η περίοδός της τείνει στο μηδέν καθώς το
αφού η περίοδός της τείνει στο μηδέν καθώς το  τείνει στο μηδέν. Μάλιστα θα παίρνει τιμές από -2 μεχρι 2 . Παρατηρώντας τον αριθμητή της παραγώγου της
τείνει στο μηδέν. Μάλιστα θα παίρνει τιμές από -2 μεχρι 2 . Παρατηρώντας τον αριθμητή της παραγώγου της  .
.  θα αλλάζει πρόσημο κάμποσες φορές στο διάστημα
θα αλλάζει πρόσημο κάμποσες φορές στο διάστημα  , όπου
, όπου  στο διάστημα
στο διάστημα ![[[0,1] [[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/e0e7f109a74b3ec224ffeb94b34335f5.png) (την γνησίως φθίνουσα ημιπερίοδο της). Η συνάρτηση σε αυτό το διάστημα είναι γνησίως φθίνουσα αλλά δεν είναι κυρτή.
(την γνησίως φθίνουσα ημιπερίοδο της). Η συνάρτηση σε αυτό το διάστημα είναι γνησίως φθίνουσα αλλά δεν είναι κυρτή.  διαμερίζουμε το διάστημα
διαμερίζουμε το διάστημα ![[0,c] [0,c]](/forum/ext/geomar/texintegr/latexrender/pictures/0b77a0c57e4d83ea934d4ef032e10c08.png) σε διαστήματα
σε διαστήματα  μήκους
μήκους  . Δηλαδή το πρώτο διάστημα θα είναι
. Δηλαδή το πρώτο διάστημα θα είναι ![d_{1}=[c-1,c] d_{1}=[c-1,c]](/forum/ext/geomar/texintegr/latexrender/pictures/880c814f9566d398d3c4b06c2ff5aef3.png) μήκους 1, το δέυτερο
μήκους 1, το δέυτερο ![d_{2}= [c -1 -\dfrac{1}{2^2},c-1] d_{2}= [c -1 -\dfrac{1}{2^2},c-1]](/forum/ext/geomar/texintegr/latexrender/pictures/8a6a6af52f2d104f140a8ca66c38bced.png) μήκους
μήκους 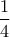 κτλ.
κτλ.
 συγκλίνει τα διαστήματα θα τείνουν όλο και πιο κοντά στο μηδέν. Από την άλλη επειδή η σειρά
συγκλίνει τα διαστήματα θα τείνουν όλο και πιο κοντά στο μηδέν. Από την άλλη επειδή η σειρά 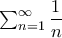 αποκλείνει η συνάρτηση καθώς θα τείνουμε στο μηδέν θα απειρίζεται.
αποκλείνει η συνάρτηση καθώς θα τείνουμε στο μηδέν θα απειρίζεται. για το οποίο το διάστημα
για το οποίο το διάστημα  θα βρίσκεται στο
θα βρίσκεται στο  , στο οποίο η συνάρτηση δεν είναι κυρτή.
, στο οποίο η συνάρτηση δεν είναι κυρτή.