![f:[0,1]\rightarrow\mathbb{R} f:[0,1]\rightarrow\mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/fe113a18e4de41c5b4fd867bf652f49a.png) δύο φορές παραγωγίσιμη έτσι ώστε να ικανοποιούνται οι εξής συνθήκες
δύο φορές παραγωγίσιμη έτσι ώστε να ικανοποιούνται οι εξής συνθήκες 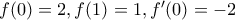 .Να δείξετε ότι υπάρχει
.Να δείξετε ότι υπάρχει  τέτοιο ώστε
τέτοιο ώστε  .
.Συντονιστής: KAKABASBASILEIOS
![f:[0,1]\rightarrow\mathbb{R} f:[0,1]\rightarrow\mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/fe113a18e4de41c5b4fd867bf652f49a.png) δύο φορές παραγωγίσιμη έτσι ώστε να ικανοποιούνται οι εξής συνθήκες
δύο φορές παραγωγίσιμη έτσι ώστε να ικανοποιούνται οι εξής συνθήκες 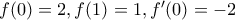 .Να δείξετε ότι υπάρχει
.Να δείξετε ότι υπάρχει  τέτοιο ώστε
τέτοιο ώστε  .
. και παρατηρούμε ότι
και παρατηρούμε ότι  . Αρκεί να βρούμε
. Αρκεί να βρούμε ![\xi \in (0,1] \xi \in (0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/79ec0d701096c22229d3b233626d896d.png) με
με  γιατί τότε, από το θεώρημα Rolle, υπάρχει
γιατί τότε, από το θεώρημα Rolle, υπάρχει  με
με  .
. έχει ρίζες στο
έχει ρίζες στο  τότε έστω
τότε έστω 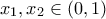 η ελάχιστη ρίζα και το ολικό ελάχιστο της
η ελάχιστη ρίζα και το ολικό ελάχιστο της  αντίστοιχα. Αφού
αντίστοιχα. Αφού  έχουμε το επιθυμητό
έχουμε το επιθυμητό ![\xi \in [x_1, x_2] \xi \in [x_1, x_2]](/forum/ext/geomar/texintegr/latexrender/pictures/96f21513d3c374ee6f153b06cd724ab3.png) .
. δεν έχει ρίζες στο
δεν έχει ρίζες στο  , ορίζουμε
, ορίζουμε  και παρατηρούμε ότι
και παρατηρούμε ότι  . Έτσι υπάρχει
. Έτσι υπάρχει  με
με  .
.
![\displaystyle{f(x)\ne 0 \forall x \in [0,1]} \displaystyle{f(x)\ne 0 \forall x \in [0,1]}](/forum/ext/geomar/texintegr/latexrender/pictures/46c5bf4245d3988f0c456fb01e10ca10.png) τότε η
τότε η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο ![\displaystyle{[0,1]} \displaystyle{[0,1]}](/forum/ext/geomar/texintegr/latexrender/pictures/1109a14ceae9f7dfdce6cfbb76246020.png) και
και  άρα υπάρχει
άρα υπάρχει  στο
στο ![\displaystyle{[0,1] :h'(a)=0 \Rightarrow \frac{1}{2}=-\frac{f'(a)}{f^2(a)}\Rightarrow g(a)=0} \displaystyle{[0,1] :h'(a)=0 \Rightarrow \frac{1}{2}=-\frac{f'(a)}{f^2(a)}\Rightarrow g(a)=0}](/forum/ext/geomar/texintegr/latexrender/pictures/1998269bc8d97b4c1e7f18152df840eb.png) και επειδή
και επειδή  πάλι με Rolle για την
πάλι με Rolle για την  στο
στο ![\displaystyle{[0,a],} \displaystyle{[0,a],}](/forum/ext/geomar/texintegr/latexrender/pictures/e82863a1b1ca05e3d44f2ae5352f9f6a.png) άρα και στο
άρα και στο ![\displaystyle{[0,1],} \displaystyle{[0,1],}](/forum/ext/geomar/texintegr/latexrender/pictures/90b0339933ef7c49ffdf807a9722cc48.png) προκύπτει εύκολα το ζητούμενο
προκύπτει εύκολα το ζητούμενο ώστε
ώστε  τότε η f δεν μπορεί να αλλάζει πρόσημο εκατέρωθεν του
τότε η f δεν μπορεί να αλλάζει πρόσημο εκατέρωθεν του  αφού
αφού  και
και  μοναδικό. Όμως τότε
μοναδικό. Όμως τότε 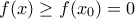 διότι
διότι 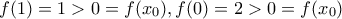 και
και
 οπότε και πάλι με Rolle στο
οπότε και πάλι με Rolle στο ![\displaystyle{[0,x_0]} \displaystyle{[0,x_0]}](/forum/ext/geomar/texintegr/latexrender/pictures/dae2d1f836be9f97d272f3a139a7c8ea.png) το ζητούμενο
το ζητούμενο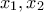 η πρώτη και η τελευταία από αυτές( η ύπαρξη πρώτης και τελευταίας τεκμηριώνεται από το γεγονός ότι υπάρχουν τουλάχιστον δυο στο
η πρώτη και η τελευταία από αυτές( η ύπαρξη πρώτης και τελευταίας τεκμηριώνεται από το γεγονός ότι υπάρχουν τουλάχιστον δυο στο ![\displaystyle{[0,1]} \displaystyle{[0,1]}](/forum/ext/geomar/texintegr/latexrender/pictures/1109a14ceae9f7dfdce6cfbb76246020.png) και η
και η  είναι συνεχής με
είναι συνεχής με  κοντά στο 0 και στο 1)
κοντά στο 0 και στο 1) για
για  ,
, κοντά στο
κοντά στο  και
και  για
για  ,
, κοντά στο
κοντά στο 

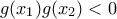 .Αρα από το θεώρημα Bolzano θα υπάρχει
.Αρα από το θεώρημα Bolzano θα υπάρχει στο
στο  Rolle και πάλι για την
Rolle και πάλι για την  στο
στο![\displaystyle{ [0,b] } \displaystyle{ [0,b] }](/forum/ext/geomar/texintegr/latexrender/pictures/e5167a68f0c2cacb5be908902f5d8422.png) δίνει το ζητούμενο.
δίνει το ζητούμενο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες