
Υ.Γ
Ενδιαφέρουσα είναι και η γενική περίπτωση :

(Χωρίς λύση )
Συντονιστής: KAKABASBASILEIOS



 [1]
[1] [2]
[2]  [3]
[3] [4]
[4] κοντα στο
κοντα στο  άτοπο απο [3] αρα
άτοπο απο [3] αρα  σε διάστημα
σε διάστημα ![\displaystyle{(-\infty,a]} \displaystyle{(-\infty,a]}](/forum/ext/geomar/texintegr/latexrender/pictures/cb6a619cda59ab04cc6c226459deae0e.png)
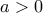 άτοπο από [1],[3]
άτοπο από [1],[3] στο
στο 
 σε διάστημα ης μορφής
σε διάστημα ης μορφής  άτοπο απο [1],[2]
άτοπο απο [1],[2] σε διάστημα
σε διάστημα ![\displaystyle{(0,b],b>0} \displaystyle{(0,b],b>0}](/forum/ext/geomar/texintegr/latexrender/pictures/2b84c886181ab99bb8da9cf8212e3299.png)
 στο
στο  ατοπο από [4] αφού
ατοπο από [4] αφού 
 στο
στο 
 είναι γν. φθίνουσα στο
είναι γν. φθίνουσα στο ![\displaystyle{(-\infty,0]} \displaystyle{(-\infty,0]}](/forum/ext/geomar/texintegr/latexrender/pictures/0c5738db64e88b1debe5ffa39effcbed.png) , εχει ολικό ελάχιστο το 0 , είναι γν αύξουσα στο
, εχει ολικό ελάχιστο το 0 , είναι γν αύξουσα στο ![\displaystyle{[0,b]} \displaystyle{[0,b]}](/forum/ext/geomar/texintegr/latexrender/pictures/af72675b110be839aefe88c0f079b878.png) οπου
οπου  'η
'η  και τελος γν φθίνουσα στό
και τελος γν φθίνουσα στό 
 συνεπως έχει 1 λυση αν
συνεπως έχει 1 λυση αν  , 2 διαφορετικες αν
, 2 διαφορετικες αν  , 3 διαφορετικες αν
, 3 διαφορετικες αν 
Εξηγήστε αν έχετε την καλοσύνη τις προτασούλες με τα κόκκινα γράμματα. Μήπως χρησιμοποιείτε κάτι σαν αντίστροφο του ΘΜΤ;R BORIS έγραψε:Eστω
Τότε
[1]
[2]
και ευκολα με DLH[3]
[4]
Ανκοντα στο
άτοπο απο [3] αρα
σε διάστημα
![\displaystyle{(-\infty,a]} \displaystyle{(-\infty,a]}](/forum/ext/geomar/texintegr/latexrender/pictures/cb6a619cda59ab04cc6c226459deae0e.png)
ανάτοπο από [1],[3]
Αρα τελικάστο
Ανσε διάστημα ης μορφής
άτοπο απο [1],[2]
Συνεπώςσε διάστημα
ανστο
ατοπο από [4] αφού
αραστο
Απο τα παραπάνω προκύπτει μεσω ενός εύκολου πινακα μονοτονίας ότι ηείναι γν. φθίνουσα στο
, εχει ολικό ελάχιστο το 0 , είναι γν αύξουσα στο
οπου
'η
και τελος γν φθίνουσα στό
Η αρχική εξίσωση γράφεταισυνεπως έχει 1 λυση αν
, 2 διαφορετικες αν
, 3 διαφορετικες αν
 ενώ είναι
ενώ είναι  . Υπάρχουν κι άλλες συνεπαγωγές για τις οποίες έχω ενστάσεις. Δεν μπορώ να βρω θεωρήματα ή αξιώματα που να τις υποστηρίζουν. Το ότι η πρώτη παράγωγος είναι αρνητική αριστερά του μηδενός πχ φαίνεται αμέσως από τον τύπο της. Το όριο της f στο πλην άπειρο δε βγαίνει με DLH. Απλώς είναι προφανές. Επίσης από τον τύπο της η
. Υπάρχουν κι άλλες συνεπαγωγές για τις οποίες έχω ενστάσεις. Δεν μπορώ να βρω θεωρήματα ή αξιώματα που να τις υποστηρίζουν. Το ότι η πρώτη παράγωγος είναι αρνητική αριστερά του μηδενός πχ φαίνεται αμέσως από τον τύπο της. Το όριο της f στο πλην άπειρο δε βγαίνει με DLH. Απλώς είναι προφανές. Επίσης από τον τύπο της η  φαίνεται ότι είναι αρνητική μετά από κάποιο b. Άρα αυτές οι συνεπαγωγές που δεν τις καταλαβαίνω είναι περιττές. Το κρισιμότερο σημείο κατά την άποψή μου είναι από 0 έως b όπου λέω πιο πάνω γιατί δεν είναι ικανοποιητική η απάντησή σας. Για να είμαι ειλικρινής στο ίδιο σημείο σκάλωσα και εγώ με την συνάρτηση
φαίνεται ότι είναι αρνητική μετά από κάποιο b. Άρα αυτές οι συνεπαγωγές που δεν τις καταλαβαίνω είναι περιττές. Το κρισιμότερο σημείο κατά την άποψή μου είναι από 0 έως b όπου λέω πιο πάνω γιατί δεν είναι ικανοποιητική η απάντησή σας. Για να είμαι ειλικρινής στο ίδιο σημείο σκάλωσα και εγώ με την συνάρτηση  που βγαίνει από την εξίσωση
που βγαίνει από την εξίσωση  λύνοντας ως προς k. Δεν καταλαβαίνω γιατί επιλέξατε την ανάποδη
λύνοντας ως προς k. Δεν καταλαβαίνω γιατί επιλέξατε την ανάποδη  .
. (ΛΑΘΟΣ)
(ΛΑΘΟΣ) (ΣΩΣΤΟ)
(ΣΩΣΤΟ)
 (ΛΑΘΟΣ)
(ΛΑΘΟΣ)  (ΣΩΣΤΟ)
(ΣΩΣΤΟ) (ΛΑΘΟΣ)
(ΛΑΘΟΣ)  (ΣΩΣΤΟ)
(ΣΩΣΤΟ) που γράφει είναι η μοναδική ρίζα της εξίσωσης
που γράφει είναι η μοναδική ρίζα της εξίσωσης 


 δίνει
δίνει  και
και  . Αν
. Αν  . Ισχυρίζεστε ότι η
. Ισχυρίζεστε ότι η  έχει μια λύση. Θα δώσω αργότερα δική μου απόδειξη ότι η
έχει μια λύση. Θα δώσω αργότερα δική μου απόδειξη ότι η  έχει ακριβώς τρεις λύσεις. Η ίδια μέθοδος δίνει ότι και η
έχει ακριβώς τρεις λύσεις. Η ίδια μέθοδος δίνει ότι και η  έχει ακριβώς τρεις λύσεις. Η πράξη δηλαδή δεν συμφωνεί μαζί σας (από το 6.7 μέχρι το 5 δε νομίζω ότι υπάρχει λάθος λόγω προσεγγίσεων)
έχει ακριβώς τρεις λύσεις. Η πράξη δηλαδή δεν συμφωνεί μαζί σας (από το 6.7 μέχρι το 5 δε νομίζω ότι υπάρχει λάθος λόγω προσεγγίσεων) που δεν περιλαμβάνει το k καθορίζει διαστήματα για το k τα οποία με τη σειρά τους θα καθορίσουν το διάγραμμα της
που δεν περιλαμβάνει το k καθορίζει διαστήματα για το k τα οποία με τη σειρά τους θα καθορίσουν το διάγραμμα της  . Οι όροι του παιχνιδιού μπαίνουν από το k.
. Οι όροι του παιχνιδιού μπαίνουν από το k.Καλησπέρα στην εκλεκτή ομήγυρη...exdx έγραψε:Να βρείτε το πλήθος των ριζών της εξίσωσης :
Υ.Γ
Ενδιαφέρουσα είναι και η γενική περίπτωση :
(Χωρίς λύση )
 .
. , παραγωγίσιμη με
, παραγωγίσιμη με  .
. είναι παραγωγίσιμη με
είναι παραγωγίσιμη με  .
.

 γνησίως αύξουσα στο
γνησίως αύξουσα στο ![(-\infty , -3 ] (-\infty , -3 ]](/forum/ext/geomar/texintegr/latexrender/pictures/78decf3ca6bed0bf2f60c60eab2b2658.png)

![g'\left ( (-\infty, -3 ) \right )= \left ( \displaystyle\lim_{x\rightarrow -\infty } g'(x),g'(-3) \right ]= (-12, -12+4e^{-3} ] g'\left ( (-\infty, -3 ) \right )= \left ( \displaystyle\lim_{x\rightarrow -\infty } g'(x),g'(-3) \right ]= (-12, -12+4e^{-3} ]](/forum/ext/geomar/texintegr/latexrender/pictures/fb45ac62a2c99d61278818b5ff9bf42d.png) .
.

 .
.

 γνησίως φθίνουσα στο
γνησίως φθίνουσα στο ![[ -3 ,-1] [ -3 ,-1]](/forum/ext/geomar/texintegr/latexrender/pictures/223efdb06ce82d1c9acb3349272901dd.png)

![g'\left ( [ -3 ,-1] \right ) = [g'(-1) , g'(-3) ] = [-12 , -12+4e^{-3} ] g'\left ( [ -3 ,-1] \right ) = [g'(-1) , g'(-3) ] = [-12 , -12+4e^{-3} ]](/forum/ext/geomar/texintegr/latexrender/pictures/570027ff41c74f93eb7e8c42112a80f0.png) .
.

 γνησίως αύξουσα στο
γνησίως αύξουσα στο 

 .
. και
και  .
. στο
στο ![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png) .
. στο
στο  τέτοιο ώστε
τέτοιο ώστε  .
. στο
στο ![(-\infty , -1] (-\infty , -1]](/forum/ext/geomar/texintegr/latexrender/pictures/a8df70f635df3bd544339aab626da347.png) και
και  γνησίως αύξουσα στο
γνησίως αύξουσα στο  .
. μοναδική ρίζα της
μοναδική ρίζα της  στο
στο  .
.  στο
στο 

 γνησίως φθίνουσα στο
γνησίως φθίνουσα στο ![(-\infty , x_{0} ] (-\infty , x_{0} ]](/forum/ext/geomar/texintegr/latexrender/pictures/b1998e79d14b320ea00b61f80ca4e646.png) .
. στο
στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) υπάρχει τουλ. 1
υπάρχει τουλ. 1  στο
στο  τέτοιο ώστε
τέτοιο ώστε  .
.![(-\infty , x_{0} ] (-\infty , x_{0} ]](/forum/ext/geomar/texintegr/latexrender/pictures/b1998e79d14b320ea00b61f80ca4e646.png) .
. στο
στο 

 γνησίως αύξουσα στο
γνησίως αύξουσα στο  .
. και μάλιστα
και μάλιστα  .
.
![\displaystyle\lim_{x\rightarrow+ \infty }\left ( x\left [ e^x\left ( x+\frac{1}{x} \right ) -12\right ] \right )=+\infty \displaystyle\lim_{x\rightarrow+ \infty }\left ( x\left [ e^x\left ( x+\frac{1}{x} \right ) -12\right ] \right )=+\infty](/forum/ext/geomar/texintegr/latexrender/pictures/ea7f6e07069161b2bd059f9b2f5d83e8.png) .
. στο
στο  .
. !
! , οπότε η
, οπότε η  έχει το ίδιο πρόσημο και τις ίδιες ρίζες με την
έχει το ίδιο πρόσημο και τις ίδιες ρίζες με την  .
. στο
στο 

 γνησίως αύξουσα στο
γνησίως αύξουσα στο ![(-\infty , x_{1} ] (-\infty , x_{1} ]](/forum/ext/geomar/texintegr/latexrender/pictures/7365b202d9c41b83a4e8b7954331ebf0.png)

![f \left ( (-\infty, x_{1} ) \right )= \left ( \displaystyle\lim_{x\rightarrow -\infty } f(x), f (x_{1} ) \right ]= (-\infty, f(x_{1}) ] f \left ( (-\infty, x_{1} ) \right )= \left ( \displaystyle\lim_{x\rightarrow -\infty } f(x), f (x_{1} ) \right ]= (-\infty, f(x_{1}) ]](/forum/ext/geomar/texintegr/latexrender/pictures/196a413256e359acc438408d9f12ef2c.png) .
. άρα
άρα  .
. ανήκει στο σύνολο τιμών της
ανήκει στο σύνολο τιμών της  συμπεραίνουμε ότι έχει ακριβώς μία ρίζα στο
συμπεραίνουμε ότι έχει ακριβώς μία ρίζα στο ![(-\infty, f(x_{1}) ] (-\infty, f(x_{1}) ]](/forum/ext/geomar/texintegr/latexrender/pictures/5404241853139e7af13e38933a52607a.png) .
. στο
στο 

 γνησίως φθίνουσα στο
γνησίως φθίνουσα στο ![[x_{1} , x_{2} ] [x_{1} , x_{2} ]](/forum/ext/geomar/texintegr/latexrender/pictures/0aff5bd80609d3d68d0e3692e352834e.png)

![f \left ( [ x_{1} , x_{2} ] \right )= \left [ f (x_{2} ) , f (x_{1} ) \right ] f \left ( [ x_{1} , x_{2} ] \right )= \left [ f (x_{2} ) , f (x_{1} ) \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/605ab422e3021e5607abfff149b66010.png) .
. άρα
άρα 

 ανήκει στο σύνολο τιμών της
ανήκει στο σύνολο τιμών της  συμπεραίνουμε ότι έχει ακριβώς μία ρίζα (δεύτερη) στο
συμπεραίνουμε ότι έχει ακριβώς μία ρίζα (δεύτερη) στο ![(x_{1} , x_{2}) ] (x_{1} , x_{2}) ]](/forum/ext/geomar/texintegr/latexrender/pictures/f6918cd7cb0793d4a1117ece634a40cb.png) .
. στο
στο 

 γνησίως αύξουσα στο
γνησίως αύξουσα στο 

 .
. ανήκει στο σύνολο τιμών της
ανήκει στο σύνολο τιμών της  συμπεραίνουμε ότι έχει ακριβώς μία ρίζα (τρίτη) στο
συμπεραίνουμε ότι έχει ακριβώς μία ρίζα (τρίτη) στο  .
.Γεια σου Κώστα.Παπαστεργίου Κώστας έγραψε:Ο υπολογιστής μου για την εξίσωσηδίνει
και
. Αν
. Ισχυρίζεστε ότι η
έχει μια λύση. Θα δώσω αργότερα δική μου απόδειξη ότι η
έχει ακριβώς τρεις λύσεις. Η ίδια μέθοδος δίνει ότι και η
έχει ακριβώς τρεις λύσεις. Η πράξη δηλαδή δεν συμφωνεί μαζί σας (από το 6.7 μέχρι το 5 δε νομίζω ότι υπάρχει λάθος λόγω προσεγγίσεων)
Η βασική μου απορία την οποία δεν ήθελα να διατυπώσω εξ αρχής είναι πως το διάγραμμα τηςπου δεν περιλαμβάνει το k καθορίζει διαστήματα για το k τα οποία με τη σειρά τους θα καθορίσουν το διάγραμμα της
. Οι όροι του παιχνιδιού μπαίνουν από το k.
Θα ανεβάσω την απόδειξη που υποσχέθηκα λίγο αργότερα (είναι λίγο μακροσκελής). Θα ήμουν υποχρεωμένος αν τύχαινε της προσοχής σας.
Ευχαριστίες
ΠΚ
![f(-\infty ,0]=[0,\infty ) f(-\infty ,0]=[0,\infty )](/forum/ext/geomar/texintegr/latexrender/pictures/0777d1b7ec24b3918fdd68a7aab22561.png)
![f[0,b]=[0,f(b)] f[0,b]=[0,f(b)]](/forum/ext/geomar/texintegr/latexrender/pictures/4eaee9b9b56906886c9722e1c057c239.png)
![f[b,\infty )=(0,f(b)] f[b,\infty )=(0,f(b)]](/forum/ext/geomar/texintegr/latexrender/pictures/bec8ce9e7550321ce48277883ae798fb.png)
 τότε ενδιαφερόμαστε για τις ρίζες της.
τότε ενδιαφερόμαστε για τις ρίζες της.


 εύκολα με DLH
εύκολα με DLH![(-\infty ,0] (-\infty ,0]](/forum/ext/geomar/texintegr/latexrender/pictures/f9d75a40b8eadac31117745d2255ef61.png) ,
,  και
και 
 είναι θετική. Άρα αριστερά του μηδενός υπάρχει ακριβώς μια ρίζα.
είναι θετική. Άρα αριστερά του μηδενός υπάρχει ακριβώς μια ρίζα.  (Rolle). Οι ρίζες όμως της
(Rolle). Οι ρίζες όμως της  είναι δεξιά του μηδενός. Έτσι η
είναι δεξιά του μηδενός. Έτσι η  θα είχε δυο ρίζες δεξιά του μηδενός και προφανώς μεταξύ -1 και 1 δηλαδή θα είχε δυο ρίζες μεταξύ 0 και 1. Τέλος η τρίτη παράγωγος
θα είχε δυο ρίζες δεξιά του μηδενός και προφανώς μεταξύ -1 και 1 δηλαδή θα είχε δυο ρίζες μεταξύ 0 και 1. Τέλος η τρίτη παράγωγος  θα έπρεπε να έχει μία τουλάχιστον ρίζα μεταξύ 0 και 1. Αυτό όμως είναι άτοπο διότι οι ρίζες της τρίτης παραγώγου είναι εκεί που η παράσταση
θα έπρεπε να έχει μία τουλάχιστον ρίζα μεταξύ 0 και 1. Αυτό όμως είναι άτοπο διότι οι ρίζες της τρίτης παραγώγου είναι εκεί που η παράσταση  είναι θετική δηλαδή εκτός του διαστήματος των 0 και 1. Άρα και στο δεύτερο διάστημα έχουμε ακριβώς μια ρίζα.
είναι θετική δηλαδή εκτός του διαστήματος των 0 και 1. Άρα και στο δεύτερο διάστημα έχουμε ακριβώς μια ρίζα. . Στην ουσία το πρόβλημά μας είναι οι τομές των διαγραμμάτων των συναρτήσεων
. Στην ουσία το πρόβλημά μας είναι οι τομές των διαγραμμάτων των συναρτήσεων  και
και  εκ των οποίων η πρώτη είναι παντού κυρτή ενώ η δεύτερη είναι κοίλη δεξιά του 1 όπως φαίνεται από το πρόσημο της
εκ των οποίων η πρώτη είναι παντού κυρτή ενώ η δεύτερη είναι κοίλη δεξιά του 1 όπως φαίνεται από το πρόσημο της  . Για τις συναρτήσεις αυτές έχουμε ακόμη ότι τέμνονται δεξιά του 1 και ότι
. Για τις συναρτήσεις αυτές έχουμε ακόμη ότι τέμνονται δεξιά του 1 και ότι  όπως δείξαμε στην αρχή. Επιπλέον είναι και οι δυο γνησίως αύξουσες. Υπό τις προϋποθέσεις αυτές θα δείξουμε ότι οι εν λόγω συναρτήσεις δεν έχουν άλλα κοινά σημεία δεξιά του 1. Η απόδειξη έχει γεωμετρικό άρωμα οπότε καλό είναι να βλέπουμε και το σχήμα Στο διάστημα από 1 έως α έχουμε τα εξής:
όπως δείξαμε στην αρχή. Επιπλέον είναι και οι δυο γνησίως αύξουσες. Υπό τις προϋποθέσεις αυτές θα δείξουμε ότι οι εν λόγω συναρτήσεις δεν έχουν άλλα κοινά σημεία δεξιά του 1. Η απόδειξη έχει γεωμετρικό άρωμα οπότε καλό είναι να βλέπουμε και το σχήμα Στο διάστημα από 1 έως α έχουμε τα εξής: Αντίθετα για την κοίλη h θα είναι
Αντίθετα για την κοίλη h θα είναι  . Είναι όμως
. Είναι όμως  οπότε
οπότε  . Αυτό σημαίνει ότι από το α και δεξιά η εφαπτομένη της κυρτής είναι πάνω από την εφαπτομένη της κοίλης. Το διάγραμμα όμως της κυρτής είναι πάνω από αυτή και το αντίθετο συμβαίνει με την κοίλη. Άρα τα διαγράμματα των συναρτήσεων δεν τέμνονται μετά το α.
. Αυτό σημαίνει ότι από το α και δεξιά η εφαπτομένη της κυρτής είναι πάνω από την εφαπτομένη της κοίλης. Το διάγραμμα όμως της κυρτής είναι πάνω από αυτή και το αντίθετο συμβαίνει με την κοίλη. Άρα τα διαγράμματα των συναρτήσεων δεν τέμνονται μετά το α. ακριβώς τρεις λύσεις.
ακριβώς τρεις λύσεις. .
. . Έτσι και στην περίπτωση k=5 έχουμε ακριβώς τρεις λύσεις.
. Έτσι και στην περίπτωση k=5 έχουμε ακριβώς τρεις λύσεις.  μερικές παρατηρήσεις. Πρώτον για οποιονδήποτε θετικό k επειδή
μερικές παρατηρήσεις. Πρώτον για οποιονδήποτε θετικό k επειδή 
 υπάρχει πάντα μία λύση. Ο k όπως και ο αριθμός 6 κανονίζει αν η f δεξιά του μηδενός θα έχει η όχι αρνητικές τιμές. Σε περίπτωση που δεν υπάρχουν αρνητικές τιμές υπάρχει μόνο η αρχική λύση αριστερά του μηδενός. Αν υπάρχουν αρνητικές τιμές οι λύσεις θα είναι ακριβώς τρεις. Υπάρχει και η περίπτωση να έχουμε μόνο δυο λύσεις μια και μια εκατέρωθεν του 0 . Μία προσέγγιση των καταλλήλων k μπορεί να γίνει με την ανισότητα
υπάρχει πάντα μία λύση. Ο k όπως και ο αριθμός 6 κανονίζει αν η f δεξιά του μηδενός θα έχει η όχι αρνητικές τιμές. Σε περίπτωση που δεν υπάρχουν αρνητικές τιμές υπάρχει μόνο η αρχική λύση αριστερά του μηδενός. Αν υπάρχουν αρνητικές τιμές οι λύσεις θα είναι ακριβώς τρεις. Υπάρχει και η περίπτωση να έχουμε μόνο δυο λύσεις μια και μια εκατέρωθεν του 0 . Μία προσέγγιση των καταλλήλων k μπορεί να γίνει με την ανισότητα  η οποία προκύπτει από τη γνωστή σχέση
η οποία προκύπτει από τη γνωστή σχέση  . Έτσι όταν η
. Έτσι όταν η  έχει αρνητικές τιμές τότε έχει και η f. Για να γίνει αυτό πρέπει
έχει αρνητικές τιμές τότε έχει και η f. Για να γίνει αυτό πρέπει  . Για να μην έχει αρνητικές τιμές είναι αρκετό το
. Για να μην έχει αρνητικές τιμές είναι αρκετό το  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: exdx και 3 επισκέπτες