Συνεχής παράγωγος (;)

#1

Η άσκηση:
Έστω συνάρτηση $f:\,\mathbb{R}\longrightarrow\mathbb{R}$ δύο φορές παραγωγίσιμη με συνεχή f''

και

.
Έστω η συνάρτηση $g:\,\mathbb{R}\longrightarrow\mathbb{R}$ με $g(x)=\left\{{\begin{array}{lc} \dfrac{f(x)}{x}\,,& x\neq0\\\noalign{\vspace{0.2cm}} f'(0)\,,& x=0 \end{array}}\right.\,.$
Να αποδειχθεί ότι η

είναι συνεχής.

Οι παρατηρήσεις:
α) Η άσκηση δόθηκε ακριβώς όπως παραπάνω.
β) Δεν μπόρεσα να αποδείξω την συνέχεια της παραγώγου

στο

, αλλά παρακάτω δίνω αυτό που σκέφτηκα.

Η απόπειρα: 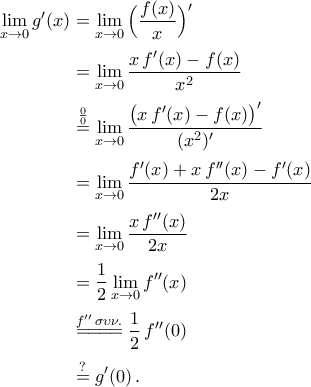$\begin{aligned} \mathop{\lim}\limits_{x\to0}g'(x)&=\mathop{\lim}\limits_{x\to0}\Big(\frac{f(x)}{x}\Big)'\\\noalign{\vspace{0.1cm}} &=\mathop{\lim}\limits_{x\to0}\frac{x\,f'(x)-f(x)}{x^2}\\\noalign{\vspace{0.1cm}} &\stackrel{\frac{0}{0}}{=}\mathop{\lim}\limits_{x\to0}\frac{\big(x\,f'(x)-f(x)\big)'}{(x^2)'} \\\noalign{\vspace{0.1cm}} &=\mathop{\lim}\limits_{x\to0}\frac{f'(x)+x\,f''(x)-f'(x)}{2x}\\\noalign{\vspace{0.1cm}} &=\mathop{\lim}\limits_{x\to0}\frac{x\,f''(x)}{2x}\\\noalign{\vspace{0.1cm}} &=\frac{1}{2}\mathop{\lim}\limits_{x\to0}f''(x)\\\noalign{\vspace{0.1cm}} &\stackrel{f''\,\sigma\upsilon\nu.}{=\!=\!=\!=}\frac{1}{2}\,f''(0)\\\noalign{\vspace{0.1cm}} &\stackrel{?}{=}g'(0)\,. \end{aligned}$ Η ερώτηση:
Υπάρχει τρόπος να αποδειχθεί ότι $g'(0)= \frac{1}{2}\,f''(0)$ ;

dement · #2

Περιληπτικά, ο λόγος μεταβολής $\displaystyle \frac{\frac{f(x)}{x}-f'(0)}{x}}$ ισούται με $\displaystyle \frac{1}{2} f''(\xi), \xi \in (0, x)$ από το θεώρημα Taylor, που μπορεί να αναχθεί σε ΘΜΤ. Η συνέχεια της δεύτερης παραγώγου κάνει τα υπόλοιπα.

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #3

Γεια σου Γρηγόρη-Δημήτρη
Νομίζω ότι πάει έτσι

$g'(0)=\lim_{x\rightarrow 0}\dfrac{\frac{f(x)}{x}-f'(0)}{x}=\lim_{x\rightarrow 0}\dfrac{f(x)-xf'(0)}{x^{2}}$

Κάνουμε DHL και το τελευταίο όριο είναι

$\lim_{x\rightarrow 0}\dfrac{f'(x)-f'(0)}{2x}=\frac{1}{2}f''(0)$

Συνεχής παράγωγος (;)

Συνεχής παράγωγος (;)

Re: Συνεχής παράγωγος (;)

Re: Συνεχής παράγωγος (;)

Μέλη σε σύνδεση