 έχει ακριβώς μία ρίζα στο
έχει ακριβώς μία ρίζα στο 
Συντονιστής: KAKABASBASILEIOS
Εστωgeorge visvikis έγραψε: ↑Τρί Οκτ 10, 2017 10:53 amΝα δείξετε ότι η εξίσωσηέχει ακριβώς μία ρίζα στο


 τότε η
τότε η 


 είναι κυρτή οπότε έχει το πολύ δύο ρίζες στο
είναι κυρτή οπότε έχει το πολύ δύο ρίζες στο 
 .
. και
και 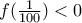
 που είναι και η μοναδική στο
που είναι και η μοναδική στο 
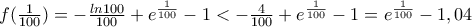


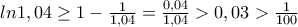
Μέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot] και 8 επισκέπτες