Λάμπρος Κατσάπας έγραψε: ↑Δευ Ιαν 15, 2018 9:44 pm
Σταμ. Γλάρος έγραψε: ↑Δευ Ιαν 15, 2018 8:06 pm
Καλησπέρα στην εκλεκτή παρέα.
Αν αντί για την υπόθεση

θεωρήσουμε το εξής :
υπάρχει

ώστε

,
τότε, νομίζω, δεν έχουμε πρόβλημα...
Αυτό έχω την αίσθηση ότι εννοεί ο Ηλίας γράφοντας:
"Θα πρέπει επιπλέον η παράγωγος να πιάνει την τιμή 1 για να συμβεί αυτό."
Ναι, αν πιάσει την τιμή 1 τότε είναι εντάξει. Μια απόδειξη έχω κάνει εδώ:
https://www.facebook.com/groups/1190609 ... 579742288/
Αν υπάρξει πιο σύντομη λύση θα χαρώ να την δω. Καλό βράδυ.
Καλησπέρα. Μια προσπάθεια. Δεν ξέρω αν είναι πιο σύντομη ...
Θεωρώ την συνάρτηση

στο
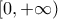
. Είναι

και

.
Αφού η

είναι κυρτή συμπεραίνουμε ότι η

είναι γνησίως αύξουσα στο
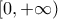
.
Εύκολα από τον ορισμό προκύπτει ότι και η
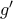
είναι γνησίως αύξουσα στο
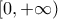
.
Άρα και η

είναι κυρτή.
Τώρα επειδή

και
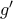
είναι γνησίως αύξουσα στο
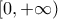
έχουμε :
α) Για



. Συνεπώς η

είναι γνησίως φθίνουσα στο
![[0,\xi] [0,\xi]](/forum/ext/geomar/texintegr/latexrender/pictures/691a2e9abf2eb71759de66d14b9cda0d.png)
.
Άρα για
 (1)
(1)
β) Για



. Συνεπώς η

είναι γνησίως αύξουσα στο
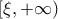
.
Έστω

. Η εξίσωση της εφαπτομένης της

στο σημείο

είναι:

και αφού η

είναι κυρτή είναι

.
Στη συνέχεια έχουμε επειδή η
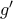
είναι γνησίως αύξουσα ότι

.
Άρα και
![\lim_{x\rightarrow +\infty }\left [ g'(x_o)(x-x_o)+g(x_o) \right ]=+\infty \lim_{x\rightarrow +\infty }\left [ g'(x_o)(x-x_o)+g(x_o) \right ]=+\infty](/forum/ext/geomar/texintegr/latexrender/pictures/4f9214af2f417b25bcfcd3b74a58cb89.png)
.
Επομένως υπάρχει

ώστε

,
οπότε και
 (2)
(2) .
Από τις
(1) και
(2) προκύπτει ότι ισχύουν οι προϋποθέσεις του Θ. Bolzano
για την

στο
![[x_1 , x_2 ] [x_1 , x_2 ]](/forum/ext/geomar/texintegr/latexrender/pictures/06376a4dd073f7a1a8a5767ba83301e0.png)
. Συνεπώς υπάρχει τουλάχιστον μία ρίζα της

στο

.
Έστω τώρα ότι η

έχει τρεις ρίζες
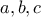
στο
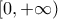
.
Εφαρμόζοντας δύο φορές το Θ. Rolle στην

στα
![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png)
και
![[b,c] [b,c]](/forum/ext/geomar/texintegr/latexrender/pictures/238bb374974bd3b5bf3b51c245fb1bdc.png)
συπμεραίνουμε ότι υπάρχουν

και

ώστε

.
Άτοπο διότι η
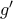
είναι γνησίως αύξουσα.
Άρα η

έχει ακριβώς δύο ρίζες στο
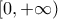
.
Φιλικά
Σταμ. Γλάρος
 που είναι κυρτή και γνήσια αύξουσα στο διάστημα
που είναι κυρτή και γνήσια αύξουσα στο διάστημα  .
.  να δειχτεί ότι η γραφική παράσταση της
να δειχτεί ότι η γραφική παράσταση της  και η ευθεία
και η ευθεία  έχουν ακριβώς δύο κοινά σημεία.
έχουν ακριβώς δύο κοινά σημεία.
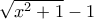 . Η άσκηση είναι του συνάδελφου Ηλία Αγγελάκου.
. Η άσκηση είναι του συνάδελφου Ηλία Αγγελάκου.


 θέλουμε.
θέλουμε. θεωρήσουμε το εξής :
θεωρήσουμε το εξής :  ώστε
ώστε  ,
, στο
στο 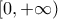 . Είναι
. Είναι  και
και  .
. είναι κυρτή συμπεραίνουμε ότι η
είναι κυρτή συμπεραίνουμε ότι η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 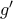 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  είναι κυρτή.
είναι κυρτή.

 . Συνεπώς η
. Συνεπώς η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![[0,\xi] [0,\xi]](/forum/ext/geomar/texintegr/latexrender/pictures/691a2e9abf2eb71759de66d14b9cda0d.png) .
.

 . Συνεπώς η
. Συνεπώς η 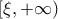 .
. . Η εξίσωση της εφαπτομένης της
. Η εξίσωση της εφαπτομένης της  είναι:
είναι: και αφού η
και αφού η  .
. .
.![\lim_{x\rightarrow +\infty }\left [ g'(x_o)(x-x_o)+g(x_o) \right ]=+\infty \lim_{x\rightarrow +\infty }\left [ g'(x_o)(x-x_o)+g(x_o) \right ]=+\infty](/forum/ext/geomar/texintegr/latexrender/pictures/4f9214af2f417b25bcfcd3b74a58cb89.png) .
. ώστε
ώστε  ,
,
 στο
στο ![[x_1 , x_2 ] [x_1 , x_2 ]](/forum/ext/geomar/texintegr/latexrender/pictures/06376a4dd073f7a1a8a5767ba83301e0.png) . Συνεπώς υπάρχει τουλάχιστον μία ρίζα της
. Συνεπώς υπάρχει τουλάχιστον μία ρίζα της  .
.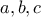 στο
στο ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) και
και ![[b,c] [b,c]](/forum/ext/geomar/texintegr/latexrender/pictures/238bb374974bd3b5bf3b51c245fb1bdc.png) συπμεραίνουμε ότι υπάρχουν
συπμεραίνουμε ότι υπάρχουν  και
και  ώστε
ώστε  .
.

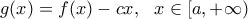
 η οποία είναι αύξουσα εφόσον f' αύξουσα (f κυρτή). Άρα g κυρτή.
η οποία είναι αύξουσα εφόσον f' αύξουσα (f κυρτή). Άρα g κυρτή. Άρα g φθίνουσα στο
Άρα g φθίνουσα στο ![\left [ a,k \right ] \left [ a,k \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/6332db0f09d3ab7279f28c8d7200c481.png)
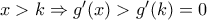 Άρα g αύξουσα στο
Άρα g αύξουσα στο 

![g([a,k))=(g(k),g(a)]\Rightarrow \boxed{g([a,k))=(g(k),0]} g([a,k))=(g(k),g(a)]\Rightarrow \boxed{g([a,k))=(g(k),0]}](/forum/ext/geomar/texintegr/latexrender/pictures/1104a46c3f71066ab96e61ae7bc1c7ff.png)

