 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με
με 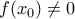 , να δειχθεί ότι
, να δειχθεί ότι 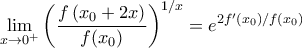
Συντονιστής: KAKABASBASILEIOS
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με
με 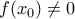 , να δειχθεί ότι
, να δειχθεί ότι 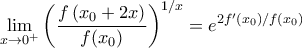

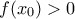 (αλλιώς δουλεύουμε με την
(αλλιώς δουλεύουμε με την  ). Λόγω συνέχειας της
). Λόγω συνέχειας της  στο σημείο
στο σημείο 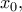 για
για 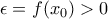 υπάρχει
υπάρχει  ώστε
ώστε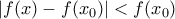 για όλα τα
για όλα τα 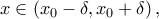 δηλαδή
δηλαδή 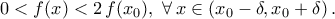
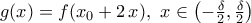 και για την οποία έχω
και για την οποία έχω 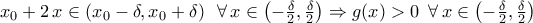
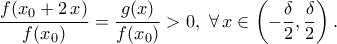
Πρώτα απ' όλα ας βελτιώσουμε την εκφώνηση γιατί χάνει σε κομψότητα: Πηγαίνοντας στο αριστερό μέλος το
 του εκθέτη δεξιά, το αποδεικτέο γίνεται
του εκθέτη δεξιά, το αποδεικτέο γίνεται 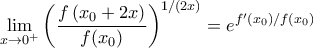
 με (νέο)
με (νέο)  , το αποδεικτέο γίνεται
, το αποδεικτέο γίνεται 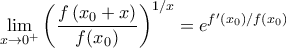
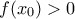 και αφού
και αφού 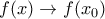 , θα είναι και
, θα είναι και 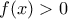 στην περιοχή του
στην περιοχή του  .
. 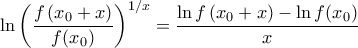
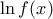 στο
στο  . Αλλά αυτή είναι
. Αλλά αυτή είναι 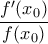 (κανόνας αλυσίδας).
(κανόνας αλυσίδας). Για
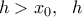 "κοντά στο
"κοντά στο 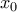 " και εφόσον η
" και εφόσον η  συνεχής, θα είναι
συνεχής, θα είναι 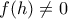
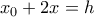 οπότε το ζητούμενο όριο είναι ίσο με το
οπότε το ζητούμενο όριο είναι ίσο με το 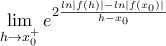
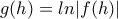 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με
με 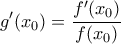 .
.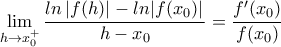 και έτσι έχουμε το ζητούμενο.
και έτσι έχουμε το ζητούμενο. μας ενδιαφέρει μόνο στο
μας ενδιαφέρει μόνο στο 


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες