Εύρεση συναρτήσεων
Συντονιστής: KAKABASBASILEIOS
-
orestisgotsis
- Δημοσιεύσεις: 1753
- Εγγραφή: Σάβ Φεβ 25, 2012 10:19 pm
Εύρεση συναρτήσεων
ΠΕΡΙΤΤΑ
τελευταία επεξεργασία από orestisgotsis σε Παρ Φεβ 23, 2024 2:24 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Λέξεις Κλειδιά:
Re: Εύρεση συναρτήσεων
Παραγωγίζοντας ως προςorestisgotsis έγραψε: ↑Παρ Ιαν 26, 2024 4:22 pmΝα βρείτε τις συναρτήσειςοι οποίες είναι ορισμένες και δύο φορές παραγωγίσιμες
στο, έτσι ώστε να ισχύει:
.
 έχουμε:
έχουμε: 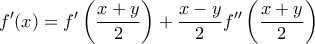
και για
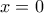 είναι
είναι 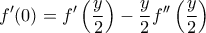
για
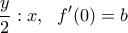 ...
...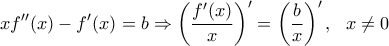
Έτσι έχουμε:
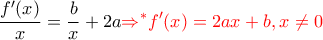 , η οποία ισχύει και για
, η οποία ισχύει και για 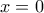
Άρα
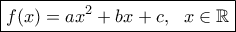 και
και  τυχαίοι πραγματικοί αριθμοί.
τυχαίοι πραγματικοί αριθμοί.Εύκολα βλέπουμε ότι οι παραπάνω συναρτήσεις ικανοποιούν την ισότητα που θέλουμε να ισχύει.
Σημείωση: Οι συναρτήσεις αυτές έχουν την εξής γεωμετρική ιδιότητα: Κάθε "χορδή" της γραφικής τους παράστασης είναι παράλληλη στην εφαπτομένη στο σημείο της γραφικής τους παράστασης με τετμημένη τη τετμημένη του μέσου της χορδής.
* :Υπάρχει μια παράλειψη, η οποία διευθετείται παρακάτω...
τελευταία επεξεργασία από abgd σε Σάβ Ιαν 27, 2024 11:14 am, έχει επεξεργασθεί 1 φορά συνολικά.


Re: Εύρεση συναρτήσεων
μια άλλη αλλαγή μεταβλητής που αφορά την συμμετρία είναι να θέσουμε
 με μεταβλητή το
με μεταβλητή το 
και παραγωγίζοντας...
μετα θα θέσουμε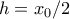 κι έτσι θα καταλήξουμε
κι έτσι θα καταλήξουμε  σταθερή...
σταθερή...
 με μεταβλητή το
με μεταβλητή το 
και παραγωγίζοντας...
μετα θα θέσουμε
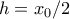 κι έτσι θα καταλήξουμε
κι έτσι θα καταλήξουμε  σταθερή...
σταθερή...Re: Εύρεση συναρτήσεων
Το αντίστροφο της πρότασης είναι εφαρμογή του σχολικού βιβλίου . Έχω πάντως την εντύπωση
ότι το πρόβλημα - όπως τέθηκε - δεν είναι κατάλληλο για τον σχολικό φάκελο ...
ότι το πρόβλημα - όπως τέθηκε - δεν είναι κατάλληλο για τον σχολικό φάκελο ...
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15768
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Εύρεση συναρτήσεων
Θα ήθελα να κάνω μικρό σχόλιο σε αυτό το βήμα: Κανονικά επιλύουμε την παραπάνω διαφορική εξίσωση χωριστά στο
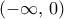 και στο
και στο 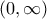 . Οπότε η σταθερά
. Οπότε η σταθερά  που βγαίνει είναι (κατ' αρχήν) διαφορετική στον ένα κλάδο από τον άλλο. Δηλαδή έχουμε αντίστοιχα
που βγαίνει είναι (κατ' αρχήν) διαφορετική στον ένα κλάδο από τον άλλο. Δηλαδή έχουμε αντίστοιχα 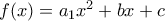 και
και 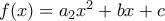 εκατέρωθεν του
εκατέρωθεν του  . Όμως μπορούμε τελικά να δείξουμε (με διάφορους τρόπους) ότι
. Όμως μπορούμε τελικά να δείξουμε (με διάφορους τρόπους) ότι 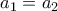 . Π.χ. για
. Π.χ. για  , οπότε τα
, οπότε τα  είναι εκατέρωθεν του
είναι εκατέρωθεν του  , η αρχική δίνει
, η αρχική δίνει 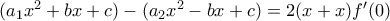 δηλαδή
δηλαδή 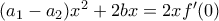 , από όπου
, από όπου 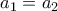 .
.Re: Εύρεση συναρτήσεων
Μιχάλη καλημέρα. Ναι....δίκιο έχεις - Απροσεξία μου.
Θα έπρεπε να το προχωρήσω ως εξής:
Είναι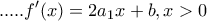 και
και 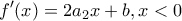
Αφού η είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  θα έχουμε:
θα έχουμε:
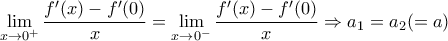
Άρα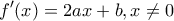 και εφόσον αυτή η ισότητα ισχύει και για
και εφόσον αυτή η ισότητα ισχύει και για 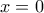 , θα είναι:
, θα είναι:
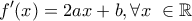
Θα έπρεπε να το προχωρήσω ως εξής:
Είναι
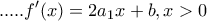 και
και 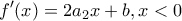
Αφού η
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  θα έχουμε:
θα έχουμε: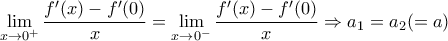
Άρα
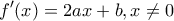 και εφόσον αυτή η ισότητα ισχύει και για
και εφόσον αυτή η ισότητα ισχύει και για 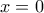 , θα είναι:
, θα είναι: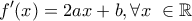


Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες

 , η οποία ισχύει και για
, η οποία ισχύει και για