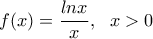 να δειχθεί η ανισότητα
να δειχθεί η ανισότητα 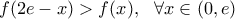
Συντονιστής: KAKABASBASILEIOS
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με παράγωγο
με παράγωγο 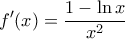 · Είναι
· Είναι 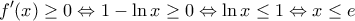
 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![(0,e] (0,e]](/forum/ext/geomar/texintegr/latexrender/pictures/1d8444b0b1caf41b600dce9babe7de1c.png) . Άρα,
. Άρα,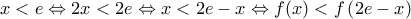

 στο διάστημα
στο διάστημα 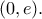 Η ζητούμενη
Η ζητούμενη  για
για  προκύπτει από την
προκύπτει από την ![ln[x(2e-x)]<2<\dfrac{x}{2e-x}+\dfrac{2e-x}{x}, ln[x(2e-x)]<2<\dfrac{x}{2e-x}+\dfrac{2e-x}{x},](/forum/ext/geomar/texintegr/latexrender/pictures/39607dc45334b0887cfaef4d9d5655f1.png)

Γιώργο ευχαριστώ για την απόδειξη....
![\displaystyle{g(x)=xln(2e-x)-(2e-x)lnx}, \ \ x\in (0,e] \displaystyle{g(x)=xln(2e-x)-(2e-x)lnx}, \ \ x\in (0,e]](/forum/ext/geomar/texintegr/latexrender/pictures/5a49fdb0d19a54da26052fff7ff2f76c.png) είναι:
είναι:![\displaystyle{g'(x)=ln(2e-x)-\frac{x}{2e-x}+lnx-\frac{2e-x}{x}= ln\left(x(2e-x)\right)- \left(\frac{x}{2e-x}+\frac{2e-x}{x}\right), \ \ x\in (0,e] \displaystyle{g'(x)=ln(2e-x)-\frac{x}{2e-x}+lnx-\frac{2e-x}{x}= ln\left(x(2e-x)\right)- \left(\frac{x}{2e-x}+\frac{2e-x}{x}\right), \ \ x\in (0,e]](/forum/ext/geomar/texintegr/latexrender/pictures/09214208b228a4753e50fb4450f79c32.png)
 , αφού οι όροι του αθροίσματος είναι θετικοί αντίστροφοι αριθμοί. Το ίσον ισχύει για
, αφού οι όροι του αθροίσματος είναι θετικοί αντίστροφοι αριθμοί. Το ίσον ισχύει για  .
.![\displaystyle{h(x)= ln\left(x(2e-x)\right), \ \ x\in (0,e] \displaystyle{h(x)= ln\left(x(2e-x)\right), \ \ x\in (0,e]](/forum/ext/geomar/texintegr/latexrender/pictures/48f27dcedbc015031d9b94f57195826d.png) και παραγωγίσουμε θα βρούμε ότι:
και παραγωγίσουμε θα βρούμε ότι: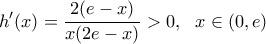 .
. είναι γνησίως αύξουσα οπότε
είναι γνησίως αύξουσα οπότε 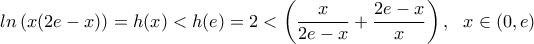
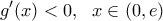 ...................
...................

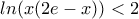 είναι ισοδύναμη προς την
είναι ισοδύναμη προς την 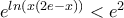 και άρα προς την
και άρα προς την 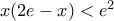 και την
και την 
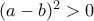 για
για 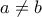 ...]
...]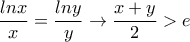 ... τότε έχουμε άμεσα την αποδεικτέα ... μέσω
... τότε έχουμε άμεσα την αποδεικτέα ... μέσω 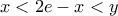 κλπ
κλπ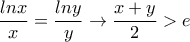 !]
!]Ναι!


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες