 και :
και :  , έχουν παράλληλες εφαπτόμενες .
, έχουν παράλληλες εφαπτόμενες .Συντονιστής: KAKABASBASILEIOS
 και :
και :  , έχουν παράλληλες εφαπτόμενες .
, έχουν παράλληλες εφαπτόμενες .Έχουν ακριβώς ένα ζεύγος από παράλληλες εφαπτόμενες καθώς
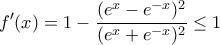 με ισότητα μόνο αν
με ισότητα μόνο αν  και
και  , η οποία ορίζεται μόνo για
, η οποία ορίζεται μόνo για  , ισχύει
, ισχύει 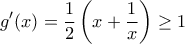 με ισότητα μόνο αν
με ισότητα μόνο αν  .
. μόνο για το ζεύγος
μόνο για το ζεύγος 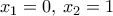 , οπότε και τα δύο μέλη είναι ίσα με
, οπότε και τα δύο μέλη είναι ίσα με  . Για όλα τα άλλα ισχύει
. Για όλα τα άλλα ισχύει 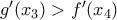 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες