Έστω μια συνάρτηση f δύο φορές παραγωγίσιμη στο [0, 2] με f(0) + f(2) = f(1). Να δείξετε ότι:
Α. Υπάρχουν
 με
με  τέτοια ώστε
τέτοια ώστε  .
.B. Αν
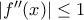 για κάθε
για κάθε  , τότε
, τότε  .
.Συντονιστής: KAKABASBASILEIOS
 με
με  τέτοια ώστε
τέτοια ώστε  .
.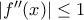 για κάθε
για κάθε  , τότε
, τότε  .
.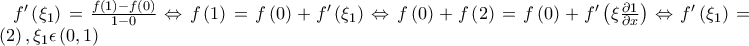


 για κάποιο
για κάποιο  κοντά στο 1. Τότε για χ=0 και χ=2 η προηγούμενη σχέση δίνει
κοντά στο 1. Τότε για χ=0 και χ=2 η προηγούμενη σχέση δίνει


 ή
ή  οπότε παίρνοντας απόλυτα και τριγωνική καταλήγουμε στην
οπότε παίρνοντας απόλυτα και τριγωνική καταλήγουμε στην  δηλαδή
δηλαδή 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες