 δύο φορές παραγωγίσιμη στο
δύο φορές παραγωγίσιμη στο  με συνεχή δεύτερη παράγωγο και με σύνολο τιμών το διάστημα
με συνεχή δεύτερη παράγωγο και με σύνολο τιμών το διάστημα ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) όπου
όπου  . Να αποδείξετε ότι:
. Να αποδείξετε ότι:(α) Υπάρχουν δύο τουλάχιστον διαφορετικά σημεία
 ώστε να ισχύει ότι:
ώστε να ισχύει ότι: 
(β) Η εξίσωση
 έχει μία τουλάχιστον πραγματική ρίζα
έχει μία τουλάχιστον πραγματική ρίζα(γ) Η εξίσωση
![f{'}{'}(x)+[f{'}(x)]^{2}=0 f{'}{'}(x)+[f{'}(x)]^{2}=0](/forum/ext/geomar/texintegr/latexrender/pictures/65c9e5cfc72821f64fd9a41a612f8286.png)
έχει επίσης μία τουλάχιστον πραγματική ρίζα.
2. Δίνεται η συνεχής και γνησίως αύξουσα στο
 συνάρτηση
συνάρτηση  με
με και
και 
Θεωρούμε την συνάρτηση
 με
με ,
, 
(α) Να μελετηθεί η
 ως προς την μονοτονία
ως προς την μονοτονία(β) Να αποδείξετε ότι υπάρχει ένα τουλάχιστον
 ώστε να ισχύει ότι:
ώστε να ισχύει ότι: 
(γ) Να αποδειχθεί ότι η εξίσωση
 έχει μία ακριβώς πραγματική ρίζα .
έχει μία ακριβώς πραγματική ρίζα .3. (α) Δίνεται η συνεχής συνάρτηση
![{f:[0,1]\rightarrow \mathbb R} {f:[0,1]\rightarrow \mathbb R}](/forum/ext/geomar/texintegr/latexrender/pictures/d14bf3fe628808a7510dc4715ef169e8.png) με
με 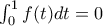 .
.Να αποδείξετε ότι υπάρχει ένα τουλάχιστον
 ώστε να ισχύει:
ώστε να ισχύει:
(β) Θεωρούμε την παραγωγίσιμη στο
 συνάρτηση
συνάρτηση  για την οποία ισχύει ότι:
για την οποία ισχύει ότι:  για κάθε
για κάθε  καθώς και την συνάρτηση
καθώς και την συνάρτηση  για κάθε
για κάθε  .
.(ι) Να αποδείξετε ότι υπάρχουν
 και
και 
(ιι) Να βρεθεί ο τύπος της

(iii) Να υπολογίσετε το

Ιωάννου Δημήτρης

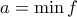 ,
,  στο από Fermat έπεται το ζητούμενο
στο από Fermat έπεται το ζητούμενο στο
στο ![[\kappa,\lambda] [\kappa,\lambda]](/forum/ext/geomar/texintegr/latexrender/pictures/9bb5b0a88d62b65815cc28e79b040cfc.png)

 πάλι με ΘΒ στο
πάλι με ΘΒ στο 
 λόγω συνέχειας κοντά στο
λόγω συνέχειας κοντά στο 
 αρα η
αρα η  άτοπο
άτοπο " για την
" για την  αλλα νομίζω ότι καλύτερα να δοθούν
αλλα νομίζω ότι καλύτερα να δοθούν  αφού
αφού  στο
στο ![[2,3] [2,3]](/forum/ext/geomar/texintegr/latexrender/pictures/d5138fec13c27bb6c645b29cdfa97a84.png)
 είναι αύξουσα και έχει προφανή ρίζα το
είναι αύξουσα και έχει προφανή ρίζα το 
![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) στην
στην 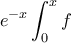
![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png) και
και  ,
, 

 ,
,  και πρόσθεση κατα μέλη . Τελικά
και πρόσθεση κατα μέλη . Τελικά 