 και
και  .
.Υ.Γ. Η λύση να γίνει διδακτικά και αναλυτικά με μελέτη των γραφικών παραστάσεων, χωρίς χρήση λογισμικού.
Συντονιστής: R BORIS
 και
και  .
.dimplak έγραψε:Να βρεθεί το εμβαδόν του χωρίου που περικλείεται μεταξύ των γραφικών παραστάσεων των συναρτήσεωνκαι
.
Υ.Γ. Η λύση να γίνει διδακτικά και αναλυτικά με μελέτη των γραφικών παραστάσεων, χωρίς χρήση λογισμικού.
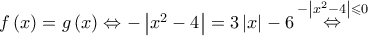






 είναι το ζητούμενο εμβαδόν τότε:
είναι το ζητούμενο εμβαδόν τότε: ![E = \int\limits_{ - 2}^2 {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \mathop = \limits^{{x^2} - 4 \leqslant 0,\forall x \in \left[ { - 2,2} \right]} \ldots \int\limits_{ - 2}^2 {\left| {{{\left| x \right|}^2} - 3\left| x \right| + 2} \right|dx} E = \int\limits_{ - 2}^2 {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \mathop = \limits^{{x^2} - 4 \leqslant 0,\forall x \in \left[ { - 2,2} \right]} \ldots \int\limits_{ - 2}^2 {\left| {{{\left| x \right|}^2} - 3\left| x \right| + 2} \right|dx}](/forum/ext/geomar/texintegr/latexrender/pictures/1ef324c69b95d11c9a1b20cf4b0d7833.png)
![\mathop = \limits^{h\left( x \right) = {{\left| x \right|}^2} - 3\left| x \right| + 2\,\,\alpha \rho \tau \iota \alpha \,\,\sigma \tau o\,\,\left[ { - 2,2} \right]} 2\int\limits_0^2 {\left| {{{\left| x \right|}^2} - 3\left| x \right| + 2} \right|dx} \mathop = \limits^{x \in \left[ {0,2} \right] \Rightarrow \left| x \right| = x} \mathop = \limits^{h\left( x \right) = {{\left| x \right|}^2} - 3\left| x \right| + 2\,\,\alpha \rho \tau \iota \alpha \,\,\sigma \tau o\,\,\left[ { - 2,2} \right]} 2\int\limits_0^2 {\left| {{{\left| x \right|}^2} - 3\left| x \right| + 2} \right|dx} \mathop = \limits^{x \in \left[ {0,2} \right] \Rightarrow \left| x \right| = x}](/forum/ext/geomar/texintegr/latexrender/pictures/45e43fdda5667825458eeef945329265.png)
![2\int\limits_0^2 {\left| {{x^2} - 3x + 2} \right|dx} \mathop = \limits^{{x^2} - 3x + 2 \geqslant 0,\forall x \in \left[ {0,1} \right],{x^2} - 3x + 2 \leqslant 0,\forall x \in \left[ {1,2} \right]} 2\int\limits_0^2 {\left| {{x^2} - 3x + 2} \right|dx} \mathop = \limits^{{x^2} - 3x + 2 \geqslant 0,\forall x \in \left[ {0,1} \right],{x^2} - 3x + 2 \leqslant 0,\forall x \in \left[ {1,2} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/4e4b9331d7e8e28d7b565367ffd114b2.png)

![2\left( {\left[ {\dfrac{{{x^3}}}{3} - 3\dfrac{{{x^2}}}{2} + 2x} \right]_0^1 + \left[ { - \dfrac{{{x^3}}}{3} + 3\dfrac{{{x^2}}}{2} - 2x} \right]_1^2} \right) = 2\left( {\left[ {\dfrac{{{x^3}}}{3} - 3\dfrac{{{x^2}}}{2} + 2x} \right]_0^1 + \left[ { - \dfrac{{{x^3}}}{3} + 3\dfrac{{{x^2}}}{2} - 2x} \right]_1^2} \right) =](/forum/ext/geomar/texintegr/latexrender/pictures/1f71834071ab4d2474f5f6b5a462612d.png)
![2\left[ {\dfrac{1}{3} - \dfrac{3}{2} + 2 - \dfrac{8}{3} + \dfrac{{12}}{2} - 4 - \left( { - \dfrac{1}{3} + \dfrac{3}{2} - 2} \right)} \right] \Rightarrow \ldots \boxed{E = 2\tau .\mu } 2\left[ {\dfrac{1}{3} - \dfrac{3}{2} + 2 - \dfrac{8}{3} + \dfrac{{12}}{2} - 4 - \left( { - \dfrac{1}{3} + \dfrac{3}{2} - 2} \right)} \right] \Rightarrow \ldots \boxed{E = 2\tau .\mu }](/forum/ext/geomar/texintegr/latexrender/pictures/511ff4039bc3213026a55f8972c80ec0.png) και το ζητούμενο έχει υπολογιστεί.
και το ζητούμενο έχει υπολογιστεί. χρησιμοποιώντας πίνακα προσήμων για κάθε παράσταση που εμφανίζεται σε απόλυτο.
χρησιμοποιώντας πίνακα προσήμων για κάθε παράσταση που εμφανίζεται σε απόλυτο. .
. καθώς και την μοναδικότητα των ριζών που υπολογίσαμε πριν, αρκεί να συγκρίνουμε τις τιμές
καθώς και την μοναδικότητα των ριζών που υπολογίσαμε πριν, αρκεί να συγκρίνουμε τις τιμές  και
και  .
. , άρα και η συνάρτηση
, άρα και η συνάρτηση  και να αφιερώσουμε λίγο χρόνο να δείξουμε ότι :
και να αφιερώσουμε λίγο χρόνο να δείξουμε ότι :
 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης