![[1,3] [1,3]](/forum/ext/geomar/texintegr/latexrender/pictures/689e1b934020b6eb3917c155d94a9a0f.png)
Δείξτε ότι το μπλε είναι μικρότερο απ΄το κόκκινο
Συντονιστής: R BORIS
![[1,3] [1,3]](/forum/ext/geomar/texintegr/latexrender/pictures/689e1b934020b6eb3917c155d94a9a0f.png)



 Mπλε Εμβαδόν
Mπλε Εμβαδόν 
![\displaystyle \int_{1}^{3} f(x) \,dx = \int_{1}^{3} \frac{x^2}{2} \,dx = \left [ \frac{x^3}{6} \right ]_{1}^{3} = \frac{13}{3} \displaystyle \int_{1}^{3} f(x) \,dx = \int_{1}^{3} \frac{x^2}{2} \,dx = \left [ \frac{x^3}{6} \right ]_{1}^{3} = \frac{13}{3}](/forum/ext/geomar/texintegr/latexrender/pictures/c65b0bb56633021e753ffdeb0d54de51.png)
 Mπλε Εμβαδόν
Mπλε Εμβαδόν  Mπλε Εμβαδόν
Mπλε Εμβαδόν  Κόκκινο Εμβαδόν.
Κόκκινο Εμβαδόν.ενώ στην λύση εξειδικεύεται στην συγκεκριμένη συνάρτηση
Από την άλλη, η λύση εμπεριέχει τα κύρια στοιχεία αντιμετώπισης και μπορεί εύκολα να επιδιορθωθεί. Γι' αυτό δίνω μόνο το βασικό βήμα ως υπόδειξη, αλλά θα επανέλθω αν χρειαστεί:
 (με γνήσια ανισότητα εκτός για
(με γνήσια ανισότητα εκτός για  όπου έχουμε ισότητα). 'Αρα
όπου έχουμε ισότητα). 'Αρα  . Τώρα ολοκληρώνουμε.
. Τώρα ολοκληρώνουμε. Φέροντας την εφαπτόμενη στο (2,2) -- αυτό νομίζω πως έχουμε το δικαίωμα να το υποθέσουμε από το σχήμα -- δημιουργείται από αυτήν και τις
Φέροντας την εφαπτόμενη στο (2,2) -- αυτό νομίζω πως έχουμε το δικαίωμα να το υποθέσουμε από το σχήμα -- δημιουργείται από αυτήν και τις  ένα τραπέζιο (βλέπε συνημμένο) με εμβαδόν
ένα τραπέζιο (βλέπε συνημμένο) με εμβαδόν  Λόγω κυρτότητας (εφαπτόμενη κάτω από την συνάρτηση) το εμβαδόν που αντιπροσωπεύει το ολοκλήρωμα είναι μεγαλύτερο του εμβαδού του τραπεζίου.
Λόγω κυρτότητας (εφαπτόμενη κάτω από την συνάρτηση) το εμβαδόν που αντιπροσωπεύει το ολοκλήρωμα είναι μεγαλύτερο του εμβαδού του τραπεζίου. (και το τρίγωνο με κορυφές
(και το τρίγωνο με κορυφές  ) πηγαίνουμε με λίγο περισσότερο κόπο στην γενική περίπτωση αύξουσας κυρτής
) πηγαίνουμε με λίγο περισσότερο κόπο στην γενική περίπτωση αύξουσας κυρτής  (και το τραπέζιο με κορυφές
(και το τραπέζιο με κορυφές  ) -- απλώς βρίσκουμε τις τομές της εφαπτομένης στο
) -- απλώς βρίσκουμε τις τομές της εφαπτομένης στο  δηλαδή της
δηλαδή της  με τις
με τις  και
και 
 όπου μας προκύπτει 'μη κυρτό τραπέζιο': νομίζω ότι ισχύουν και πάλι τα παραπάνω (με χρήση προσημασμένων εμβαδών ας πούμε), αλλά είναι και λίγο αργά
όπου μας προκύπτει 'μη κυρτό τραπέζιο': νομίζω ότι ισχύουν και πάλι τα παραπάνω (με χρήση προσημασμένων εμβαδών ας πούμε), αλλά είναι και λίγο αργά  , και η συνάρτηση είναι κυρτή στο
, και η συνάρτηση είναι κυρτή στο 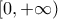 έχουμε την εξής λύση:
έχουμε την εξής λύση:



Συνεχίζοντας,
![\forall x \in \left[0,4\right]f(x) + f(4-x) \geq 2f(2) \forall x \in \left[0,4\right]f(x) + f(4-x) \geq 2f(2)](/forum/ext/geomar/texintegr/latexrender/pictures/fb39ebfc6498301bd9ef3e8cb75fa8f5.png) , τότε
, τότε


 , τότε
, τότε
 Κόκκινο Εμβαδόν
Κόκκινο Εμβαδόν  Mπλε Εμβαδόν
Mπλε Εμβαδόν 
 Mπλε Εμβαδόν
Mπλε Εμβαδόν  Κόκκινο Εμβαδόν.
Κόκκινο Εμβαδόν.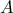 είναι μέσον του
είναι μέσον του  , έχουμε,
, έχουμε, :
:
 είναι μια αρχική της
είναι μια αρχική της 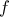 , αποδείξαμε ότι
, αποδείξαμε ότι 
 .
.Γιώργη είτε για την
 στην #7 είτε για την
στην #7 είτε για την  στην #9 χρειάζεσαι την
στην #9 χρειάζεσαι την  (#7) ή την
(#7) ή την  (#9), και αυτές εξασφαλίζονται αν και μόνον αν η εφαπτομένη στο
(#9), και αυτές εξασφαλίζονται αν και μόνον αν η εφαπτομένη στο 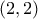 διέρχεται από τα
διέρχεται από τα  και
και  .
.Ένα 'οριακό' (αντι)παράδειγμα αποτελεί η
 , η οποία ικανοποιεί, όπως και η 'δοθείσα'
, η οποία ικανοποιεί, όπως και η 'δοθείσα'  τις
τις 
 για
για 
 για
για 
Αντιπαράδειγμα στο ότι όποια συνάρτηση ικανοποιεί τις παραπάνω συνθήκες οφείλει να είναι ηgbaloglou έγραψε: ↑Δευ Μάιος 13, 2024 11:20 pmΈνα 'οριακό' (αντι)παράδειγμα αποτελεί η, η οποία ικανοποιεί, όπως και η 'δοθείσα'
τις

για

για

 OXI στο ότι ισχύουν οι επιθυμητές και απαραίτητες ισότητες
OXI στο ότι ισχύουν οι επιθυμητές και απαραίτητες ισότητες  ή/και
ή/και  ... οι οποίες προκύπτουν εν γένει, όπως άλλωστε έμμεσα επισημαίνω στην #4, από την
... οι οποίες προκύπτουν εν γένει, όπως άλλωστε έμμεσα επισημαίνω στην #4, από την  Στο (αντι)παράδειγμα μου αντί της 'αναμενόμενης'
Στο (αντι)παράδειγμα μου αντί της 'αναμενόμενης'  ισχύει η
ισχύει η  ενώ η εφαπτομένη στο
ενώ η εφαπτομένη στο  διέρχεται από τα
διέρχεται από τα  και
και 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης