Με ποια άσκηση του σχολικού βιβλίου μοιάζει το θέμα αυτό ή αυτή η ερώτηση ;Το έλυνε ο μαθητής αν είχε λύσει αυτή(...) την άσκηση ;
Δεν σας κρύβω ότι και γω στις εξετάσεις δε φοβάμαι τίποτα πιο πολύ από το να τεθεί μια μικρή παραλλαγή ή επέκταση μας σχολικής άσκησης και να μου πουν : Να κύριε, αυτή δεν την είχαμε ξαναλύσει ή δεν την προσέξαμε !
Επειδή λοιπόν είναι από κάθε σκοπιά παράλογο οι μαθητές μας να έχουν λύσει χίλιες εξωσχολικές ασκήσεις και να χάσουν μια σχολική, άρχισα από χθες να παίρνω μία - μία τις πιο χαρακτηριστικές ασκήσεις του σχολικού και να τις κάνω θέματα ή να κρύβω τις ιδέες των ασκήσεων μέσα σε απλές κατά τα άλλα ασκήσεις - θέματα.
Θεωρώ πως θα ήταν μια εξαιρετική βοήθεια προς τους μαθητές (και τους εαυτούς μας ίσως) να συλλέξουμε όσα περισσότερα μπορούμε από αυτά τα θέματα(ή και ασκήσεις του ενός ερωτήματος).
Θα έχει νομίζω ενδιαφέρον για δύο τουλάχιστον ακόμα χρόνια !
Αρχίζω με δυο θέματα από τα ολοκληρώματα(η ιδέα είναι από τις πρώτες γενικές ασκήσεις του σχολικού) και συνεχίστε εσείς με ό,τι κρίνετε ωραίο και σημαντικό :
ΑΣΚΗΣΗ 1(γεν.2/σελ 352)
Δίνεται η συνάρτηση
 με τύπο :
με τύπο :  ,
,  .
.α) Να μελετήσετε την
 ως προς τη μονοτονία και τα κοίλα.
ως προς τη μονοτονία και τα κοίλα.β) Να βρείτε της ασύμπτωτες της γραφικής παράστασης της
 .
.γ) Να βρείτε το σύνολο τιμών της συνάρτησης
 .
.δ) Να βρείτε το εμβαδόν του χωρίου που περικλείεται από τη
 τον άξονα
τον άξονα  και τις ευθείες με εξισώσεις
και τις ευθείες με εξισώσεις  .
.Μπάμπης

 και
και 
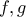 .
. είναι παραγωγίσιμες.
είναι παραγωγίσιμες.

 και
και  παραγωγίσιμες συναρτήσεις ώστε να ισχύουν
παραγωγίσιμες συναρτήσεις ώστε να ισχύουν  και
και  με
με 
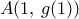 είναι η
είναι η 
 και ότι είναι κοίλη,στο
και ότι είναι κοίλη,στο  και η
και η 



 για την οποία ισχύει
για την οποία ισχύει 
 με
με  να βρείτε την εφαπτομένη
να βρείτε την εφαπτομένη  της γραφικής παράστασης της
της γραφικής παράστασης της 
 να δείξετε ότι
να δείξετε ότι 
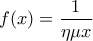 ,
,  .
.
 Λύνουμε την εξίσωση:
Λύνουμε την εξίσωση:


![\displaystyle \left(0,\frac{\pi}{2} \right] \displaystyle \left(0,\frac{\pi}{2} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/07714a269709fa34d899332d5c554fdf.png) και γνησίως αύξουσα στο
και γνησίως αύξουσα στο 
 είναι επίσης παραγωγίσιμη στο πεδίο ορισμού της οπότε:
είναι επίσης παραγωγίσιμη στο πεδίο ορισμού της οπότε:
 οπότε θα εξετάσουμε τι συμβαίνει στα άκρα του διαστήματος.
οπότε θα εξετάσουμε τι συμβαίνει στα άκρα του διαστήματος.

 και
και  είναι κατακόρυφες ασύμπτωτες της
είναι κατακόρυφες ασύμπτωτες της ![\displaystyle f(\left(0,\pi \right))=f\left(\left(0,\frac{\pi}{2} \right] \right)\cup f\left(\left(\frac{\pi}{2},\pi \right) \right)=\left[f\left(\frac{\pi}{2}\right),\lim_{x\rightarrow 0^+}f(x) \right) \cup \left(f\left(\frac{\pi}{2} \right),\lim_{x \rightarrow \pi^-}f(x) \right)=\left[1,+\infty \right)\cup \left(1,+\infty \right)=\left[1,+\infty \right) \displaystyle f(\left(0,\pi \right))=f\left(\left(0,\frac{\pi}{2} \right] \right)\cup f\left(\left(\frac{\pi}{2},\pi \right) \right)=\left[f\left(\frac{\pi}{2}\right),\lim_{x\rightarrow 0^+}f(x) \right) \cup \left(f\left(\frac{\pi}{2} \right),\lim_{x \rightarrow \pi^-}f(x) \right)=\left[1,+\infty \right)\cup \left(1,+\infty \right)=\left[1,+\infty \right)](/forum/ext/geomar/texintegr/latexrender/pictures/d4a31dd763d24271e808b2389d841deb.png)
![\displaystyle E=\int_{\frac{\pi}{3}}^{\frac{\pi}{2}}{\left|\frac{1}{\eta \mu x} \right|dx}\stackrel{\eta \mu x>0}=\int_{\frac{\pi}{3}}^{\frac{\pi}{2}}{\frac{1}{\eta \mu x} dx}= \int_{\frac{\pi}{2}}^{\frac{\pi}{3}}{\frac{\eta \mu ^2\frac{x}{2}+\sigma \upsilon \nu ^2\frac{x}{2}}{2\eta \mu \frac{x}{2}\cdot \sigma \upsilon \nu \frac{x}{2}}dx}=\int_{\frac{\pi}{3}}^{\frac{\pi}{2}}{\frac{\eta \mu \frac{x}{2}}{2\sigma \upsilon \nu \frac{x}{2}}dx}+\int_{\frac{\pi}{3}}^{\frac{\pi}{2}}{\frac{\sigma \upsilon \nu \frac{x}{2}}{2 \eta \mu \frac{x}{2}}dx} =\left[ln\left(2\eta \mu \frac{x}{2}\right) -ln\left(2\sigma \upsilon \nu \frac{x}{2} \right)\right]^{\frac{\pi}{2}}_{\frac{\pi}{3}} =\frac{ln3}{2} \displaystyle E=\int_{\frac{\pi}{3}}^{\frac{\pi}{2}}{\left|\frac{1}{\eta \mu x} \right|dx}\stackrel{\eta \mu x>0}=\int_{\frac{\pi}{3}}^{\frac{\pi}{2}}{\frac{1}{\eta \mu x} dx}= \int_{\frac{\pi}{2}}^{\frac{\pi}{3}}{\frac{\eta \mu ^2\frac{x}{2}+\sigma \upsilon \nu ^2\frac{x}{2}}{2\eta \mu \frac{x}{2}\cdot \sigma \upsilon \nu \frac{x}{2}}dx}=\int_{\frac{\pi}{3}}^{\frac{\pi}{2}}{\frac{\eta \mu \frac{x}{2}}{2\sigma \upsilon \nu \frac{x}{2}}dx}+\int_{\frac{\pi}{3}}^{\frac{\pi}{2}}{\frac{\sigma \upsilon \nu \frac{x}{2}}{2 \eta \mu \frac{x}{2}}dx} =\left[ln\left(2\eta \mu \frac{x}{2}\right) -ln\left(2\sigma \upsilon \nu \frac{x}{2} \right)\right]^{\frac{\pi}{2}}_{\frac{\pi}{3}} =\frac{ln3}{2}](/forum/ext/geomar/texintegr/latexrender/pictures/829f26263349901cf2e061fb96774238.png)
 και
και 
 έχει πεδίο ορισμού το
έχει πεδίο ορισμού το ![\mathbb{A}=\left[-1,1 \right] \mathbb{A}=\left[-1,1 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/dec6be34f781df75cfc4c4ccd5a2f6ef.png) αφού πρέπει και αρκεί
αφού πρέπει και αρκεί 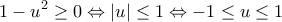
 απο όπου προκύπτει
απο όπου προκύπτει ![\displaystyle D_f=\mathbb{A}=\left[-1,1 \right] \displaystyle D_f=\mathbb{A}=\left[-1,1 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/81a90cc69ec7e9c125e29ad3ea7f5eba.png)
![\displaystyle D_g=D_f=\mathbb{A}=\left[-1,1 \right] \displaystyle D_g=D_f=\mathbb{A}=\left[-1,1 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/a57258638aed5203ab2276ab84848978.png)
 είναι συνεχής στο
είναι συνεχής στο 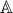 ως σύνθεση συνεχών συναρτήσεων επομένως στο ίδιο διάστημα η συνάρτηση
ως σύνθεση συνεχών συναρτήσεων επομένως στο ίδιο διάστημα η συνάρτηση  είναι παραγωγίσιμη.
είναι παραγωγίσιμη.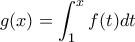 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο 
 ισχύει:
ισχύει: 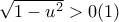

 απο ολοκλήρωση της
απο ολοκλήρωση της  στο
στο ![[x,1] [x,1]](/forum/ext/geomar/texintegr/latexrender/pictures/e6689e594cced63960b4f18d29966070.png) έχουμε:
έχουμε:
 με το ίσον να ισχύει σε ένα μεμονωμένο σημείο άρα
με το ίσον να ισχύει σε ένα μεμονωμένο σημείο άρα ![[-1,1] [-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d060b17b29e0dae91a1cac23ea62281a.png)
 και ισχύει:
και ισχύει: με το ίσον να ισχύει στα άκρα του διαστήματος άρα
με το ίσον να ισχύει στα άκρα του διαστήματος άρα  λαμβάνουμε την προφανή λύση
λαμβάνουμε την προφανή λύση ![\displaystyle E=\int_{0}^{1}{\left|f(x) \right|dx}\stackrel{f(x)\leq 0,x \in[0,1] }=-\int_{0}^{1}{f(x)dx}=-\int_{0}^{1}{(x)'f(x)dx}=-\left[xf(x) \right]_0^1+\int_{0}^{1}{xf'(x)dx}=-f(1)-\frac{1}{2}\int_{0}^{1}{\left(1-x^2 \right)'\sqrt{1-x^2}dx}\stackrel{1-x^2=u,(1-x^2)'dx=du}=-\frac{1}{2}\int_{1}^{0}{\sqrt{u}du}=\frac{1}{2}\int_{0}^{1}{u^{\frac{1}{2}}du}=\frac{1}{2}\left[\frac{2}{3}u^{\frac{3}{2}} \right]_0^1=\frac{1}{3} \displaystyle E=\int_{0}^{1}{\left|f(x) \right|dx}\stackrel{f(x)\leq 0,x \in[0,1] }=-\int_{0}^{1}{f(x)dx}=-\int_{0}^{1}{(x)'f(x)dx}=-\left[xf(x) \right]_0^1+\int_{0}^{1}{xf'(x)dx}=-f(1)-\frac{1}{2}\int_{0}^{1}{\left(1-x^2 \right)'\sqrt{1-x^2}dx}\stackrel{1-x^2=u,(1-x^2)'dx=du}=-\frac{1}{2}\int_{1}^{0}{\sqrt{u}du}=\frac{1}{2}\int_{0}^{1}{u^{\frac{1}{2}}du}=\frac{1}{2}\left[\frac{2}{3}u^{\frac{3}{2}} \right]_0^1=\frac{1}{3}](/forum/ext/geomar/texintegr/latexrender/pictures/3284f17f804b1aa8354fe964f4e401a9.png)
 , με
, με  .
. να βρείτε το πλήθος των πραγματικών ριζών της εξίσωσης
να βρείτε το πλήθος των πραγματικών ριζών της εξίσωσης  με πεδίο ορισμού το σύνολο των θετικών αριθμών που ικανοποιεί τη σχέση:
με πεδίο ορισμού το σύνολο των θετικών αριθμών που ικανοποιεί τη σχέση: 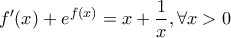 με
με  .
. , όπου
, όπου  , να αποδείξετε ότι :
, να αποδείξετε ότι : ,
, 
 ένα σημείο της
ένα σημείο της  .
.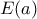 που περικλείεται από τη
που περικλείεται από τη  τη στιγμή που η τετμημένη του
τη στιγμή που η τετμημένη του  είναι
είναι  .
. για τους οποίους ισχύει ότι :
για τους οποίους ισχύει ότι : 

 δύο από τους μιγαδικούς που επαληθεύουν τη δoσμένη σχέση με
δύο από τους μιγαδικούς που επαληθεύουν τη δoσμένη σχέση με  = 4.
= 4.



 και
και  για κάθε
για κάθε 

 με
με  , να βρεθεί o τύπος της συνάρτησης αυτής.
, να βρεθεί o τύπος της συνάρτησης αυτής. που είναι συνεχής στο
που είναι συνεχής στο  και έχει την ιδιότητα :
και έχει την ιδιότητα : για κάθε
για κάθε 
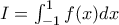
 , να βρεθεί ο τύπος της συνάρτησης
, να βρεθεί ο τύπος της συνάρτησης  είναι παραγωγίσιμη.Υποθέτουμε ότι υπάρχει αρχική
είναι παραγωγίσιμη.Υποθέτουμε ότι υπάρχει αρχική  της
της  .
. ,
,

 , αν ισχύει ότι :
, αν ισχύει ότι :

 και να αποδειχθεί ότι οι ρίζες της έχουν μετρο
και να αποδειχθεί ότι οι ρίζες της έχουν μετρο  .
. και
και 
 με
με 


 έχουν ίσα μέτρα, τότε :
έχουν ίσα μέτρα, τότε :


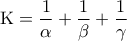

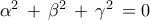 , να αποδειχθεί ότι :
, να αποδειχθεί ότι :

 είναι ομοκυκλικά σημεία.
είναι ομοκυκλικά σημεία.



