Θέμα 136

orestisgotsis · #1

Περιττό

#2

orestisgotsis έγραψε:Αν $\displaystyle{{z_1},\,{z_2}}$ οι ρίζες της εξίσωσης $\displaystyle{\left( E \right):\left( {{\lambda ^2} + 3} \right){z^2} - 4z + 2 = 0,\,\,\,\lambda \in \left( {0,\, + \infty } \right)}$ , με $\displaystyle{\left| {{z_1}} \right| = \frac{{\sqrt 2 }}{2},\,\,{\mathop{\rm Im}\nolimits} \left( {{z_1}} \right) > {\mathop{\rm Im}\nolimits} \left( {{z_2}} \right)}$ και $\displaystyle{w}$ τυχαίος μιγαδικός, τότε:

α) Να αποδειχθεί ότι $\displaystyle{\lambda = 1}$ .

β) Να υπολογισθεί το άθροισμα $\displaystyle{{z_1}^4 + {z_2}^4}$ .

γ) Να αποδειχθεί ότι $\displaystyle{\left| {w - {z_1}} \right| + \left| {w + {z_2}} \right| \ge 1}$ .

δ) Να βρεθεί ο γεωμετρικός τόπος των εικόνων των $\displaystyle{w}$ για τους οποίους ισχύει:

$\displaystyle{\left| {w - {z_1}} \right| + \left| {w - {z_2}} \right| = 1}$ .

ε) Να αποδειχθεί ότι $\displaystyle{\int\limits_0^1 {\left| {x{z_1} + {z_2}} \right|\,dx} \le \frac{{3\sqrt 2 }}{4}}$ .

Πηγή: Μαθηματικά Γ΄ Λυκείου των Ζανταρίδη – Μαυροφρύδη – Ραϊκόφτσαλη.

...και σύμφωνα με τις διορθώσεις που είχε δώσει ο Θωμάς....

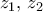α) Αφού $\displaystyle{{z_1},\,{z_2}}$ οι ρίζες της εξίσωσης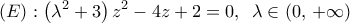 $\displaystyle{\left( E \right):\left( {{\lambda ^2} + 3} \right){z^2} - 4z + 2 = 0,\,\,\,\lambda \in \left( {0,\, + \infty } \right)}$

με πραγματικούς συντελεστές θα είναι συζυγείς μεταξύ τους άρα ${{z}_{2}}={{\bar{z}}_{1}}$ και σύμφωνα με τους τύπους του Vietta θα ισχύει ότι

${{z}_{1}}{{z}_{2}}=\frac{2}{{{\lambda }^{2}}+3}\Leftrightarrow {{z}_{1}}{{\bar{z}}_{1}}=\frac{2}{{{\lambda }^{2}}+3}\Leftrightarrow |{{z}_{1}}{{|}^{2}}=\frac{2}{{{\lambda }^{2}}+3}\Leftrightarrow \frac{1}{2}=\frac{2}{{{\lambda }^{2}}+3}\Leftrightarrow {{\lambda }^{2}}=1$

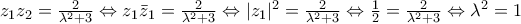
και επειδή $\lambda >0$ θα είναι $\lambda =1$

β) Η εξίσωση γίνεται $4{{z}^{2}}-4z+2=0\Leftrightarrow 2{{z}^{2}}-2z+1=0$ άρα ισχύει ότι $2z_{1}^{2}=2{{z}_{1}}-1$ (1) άρα και

$2z_{1}^{2}{{z}_{1}}=2z_{1}^{2}-{{z}_{1}}\Leftrightarrow 2z_{1}^{3}={{z}_{1}}-1$ (λόγω της (1)) άρα και $2z_{1}^{3}{{z}_{1}}=z_{1}^{2}-{{z}_{1}}$ ή

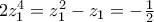$2z_{1}^{4}=z_{1}^{2}-{{z}_{1}}=-\frac{1}{2}$ (λόγω της (1)) άρα τελικά 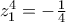$z_{1}^{4}=-\frac{1}{4}$ οπότε

${{z}_{1}}^{4}+{{z}_{2}}^{4}={{z}_{1}}^{4}+{{\bar{z}}_{1}}^{4}=-\frac{1}{2}$

γ) Είναι λύνοντας την εξίσωση ${{z}_{1}}=\frac{1}{2}+\frac{1}{2}i,\,\,\,{{z}_{2}}=\frac{1}{2}-\frac{1}{2}i$ και επειδή

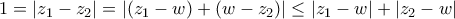$1=|{{z}_{1}}-{{z}_{2}}|=|({{z}_{1}}-w)+(w-{{z}_{2}})|\le |{{z}_{1}}-w|+|{{z}_{2}}-w|$ θα ισχύει τελικά $\left| w-{{z}_{1}} \right|+\left| w-{{z}_{2}} \right|\ge 1$

δ) Αν τώρα $M(w),\,\,\,A({{z}_{1}}),\,\,B({{z}_{2}})$ από $\left| w-{{z}_{1}} \right|+\left| w-{{z}_{2}} \right|=1$ θα έχουμε ότι

$\left| \overrightarrow{MA} \right|+\left| \overrightarrow{MB} \right|=|\overrightarrow{AB}|=|\overrightarrow{MA}-\overrightarrow{MB}|$ που σημαίνει ότι τα

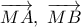$\overrightarrow{MA},\,\,\overrightarrow{MB}$ είναι αντίρροπα διανύσματα άρα

εσωτερικό σημείο του ευθυγράμμου τμήματος

$A\,B$ με $A(\frac{1}{2},\,\,\frac{1}{2}),\,\,B(\frac{1}{2},\,\,\,-\frac{1}{2})$ και τα σημεία $A,\,B$

ε) Επειδή ισχύει ότι $\left| x{{z}_{1}}+{{z}_{2}} \right|\le |x{{z}_{1}}|+|{{z}_{2}}|=|x||{{z}_{1}}|+|{{z}_{2}}|=(x+1)\frac{\sqrt{2}}{2}$ (με $x\in [0,\,\,1]$ )

θα ισχύει και η $\int\limits_{0}^{1}{\left| x{{z}_{1}}+{{z}_{2}} \right|dx}\le \frac{\sqrt{2}}{2}\int\limits_{0}^{1}{(x+1)dx}=\frac{\sqrt{2}}{2}\left[ \frac{{{x}^{2}}}{2}+x \right]_{0}^{1}=\frac{3\sqrt{2}}{4}$

Φιλικά και Μαθηματικά
Βασίλης

mathxl · #3

Καλημέρα!

Από ότι βλέπω τα γ και δ δεν χρειάζονται διόρθωση πατάνε καλά.
πχ το γ
$\left| {w - {z_1}} \right| - \left| {w - {z_2}} \right| \le \left| {\left| {w - {z_1}} \right| - \left| {w - {z_2}} \right|} \right| \le \left| {\left( {w - {z_1}} \right) - \left( {w - {z_2}} \right)} \right| = \left| {{z_2} - {z_1}} \right| = 1.$

Το δ βγαίνει ημιευθεία ( ειδική περίπτωση για συνθήκη υπερβολής) όπως είναι στο κομμάτι υποδείξεων λύσεων).

Για το (ε) έχουμε:
$\left| {x{z_1} + {z_2}} \right| = \left| {\frac{{x + 1}}{2} + \frac{{x - 1}}{2}i} \right| = \sqrt {\frac{{2{x^2} + 2}}{4}} = \frac{{\sqrt 2 }}{2}\sqrt {{x^2} + 1} \le 1$ με την ισότητα να ισχύει όταν x = 1

. Ωστόσο αυτό που θέλαμε ήταν αυτό που έκανε ο Βασίλης παραπάνω(τριγωνική).

Θέμα 136

Θέμα 136

Re: Θέμα 136

Re: Θέμα 136

Μέλη σε σύνδεση