exdx έγραψε:Έστω η παραγωγίσιμη συνάρτηση

με

και :

, για κάθε

.
Δ1) Να αποδειχθεί ότι

.
Δ2) Να μελετηθεί η

ως προς τη μονοτονία , τα ακρότατα, τα κοίλα και να βρεθεί το σύνολο τιμών της.
Δ3) Να αποδειχθεί ότι:

για κάθε

με

Δ4) Να υπολογιστεί το όριο
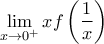
Δ5) Να αποδειχθεί ότι

για κάθε

Edit : Διορθώθηκε το Δ5 ( βλέπε επόμενη δημοσίευση )
Υ.Γ. Η πηγή μετά...
Καλησπέρα. Μια προσπάθεια στην ωραία άσκηση του Γιώργη...
Δ1)










(Η
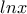
είναι 1-1.)
Άρα από Πόρισμα Συνεπειών Θ.Μ.Τ. υπάρχει σταθερά


(1)
Τώρα θεωρούμε

. Οπότε

(2),
επειδή
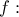
συνεχής ως παραγωγίσιμη στο

Άρα

.
Επίσης
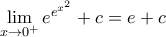
(3)
Από την (1) έχουμε :
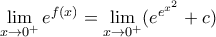
και με αντικατάσταση των (2) και (3)

, οπότε

Άρα

συνεπώς

.
Δ2) Είναι


. Άρα η

είναι γνησίως αύξουσα στο

.
και παρουσιάζει στο

, ολικό ελάχιστο το

Επίσης


.
Άρα η

είναι κυρτή στο

.
Ακόμα

, άρα το σύνολο τιμών της

είναι το
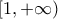
.
Δ3) Θεωρώ

. Είναι παραγωγίσιμη με

όπου

με
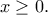
Είναι

. Άρα η

είναι γνησίως αύξουσα στο

.
Άρα για

είναι

οπότε και

άρα και

είναι γνησίως αύξουσα.
Συνεπώς
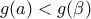
.
Δ4) Εφαρμόζοντας κανόνα de L' Ηospital έχουμε:

Θα προσπαθήσω αργότερα το Δ5 ... Μας καλεί το καθήκον!
Φιλικά
Σταμ. Γλάρος
 με
με  και :
και : , για κάθε
, για κάθε  .
. .
. ως προς τη μονοτονία , τα ακρότατα, τα κοίλα και να βρεθεί το σύνολο τιμών της.
ως προς τη μονοτονία , τα ακρότατα, τα κοίλα και να βρεθεί το σύνολο τιμών της.  για κάθε
για κάθε  με
με 
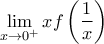
 για κάθε
για κάθε 




 (Η
(Η 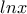 είναι 1-1.)
είναι 1-1.)
 (1)
(1) . Οπότε
. Οπότε  (2),
(2), 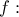 συνεχής ως παραγωγίσιμη στο
συνεχής ως παραγωγίσιμη στο 
 .
.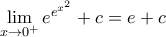 (3)
(3)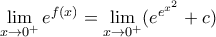
 , οπότε
, οπότε 
 συνεπώς
συνεπώς  .
.
 . Άρα η
. Άρα η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  .
. , ολικό ελάχιστο το
, ολικό ελάχιστο το 

 , άρα το σύνολο τιμών της
, άρα το σύνολο τιμών της 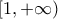 .
. . Είναι παραγωγίσιμη με
. Είναι παραγωγίσιμη με  όπου
όπου  με
με 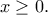
 . Άρα η
. Άρα η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  είναι
είναι  οπότε και
οπότε και  άρα και
άρα και  είναι γνησίως αύξουσα.
είναι γνησίως αύξουσα.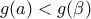 .
.
![[0,\alpha] [0,\alpha]](/forum/ext/geomar/texintegr/latexrender/pictures/7ab63225c769d29bc871e0ad6680824e.png) έχουμε ότι
έχουμε ότι ![\displaystyle{f(x)\leq 1+\frac{f(\alpha)-1}{\alpha}x, x\in[0,\alpha]}. \displaystyle{f(x)\leq 1+\frac{f(\alpha)-1}{\alpha}x, x\in[0,\alpha]}.](/forum/ext/geomar/texintegr/latexrender/pictures/87328299318bb1dc399acdf120519be9.png)
 και
και 

 στο
στο