KAKABASBASILEIOS έγραψε: ↑Τετ Σεπ 13, 2017 2:09 pm
exdx έγραψε: ↑Πέμ Σεπ 07, 2017 9:34 am
1. Δίνεται ο πίνακας κάποιων τιμών μιας συνάρτησης παραγωγίσιμης στο
![\displaystyle{[0,4]} \displaystyle{[0,4]}](/forum/ext/geomar/texintegr/latexrender/pictures/c61be56947799f444c9605b715f7960c.png)
Untitled.png
Ο πίνακας αυτός εγγυάται ότι : (Σωστό ή Λάθος ; )
α. Η συνάρτηση έχει σύνολο τιμών το
![\displaystyle{[2,5]} \displaystyle{[2,5]}](/forum/ext/geomar/texintegr/latexrender/pictures/4a861a2397252bbd9297dc495ebeccd9.png)
β. Η συνάρτηση είναι γνησίως αύξουσα στο
![\displaystyle{[0,2]} \displaystyle{[0,2]}](/forum/ext/geomar/texintegr/latexrender/pictures/ea285087bce84082ad9b0ee271285211.png)
γ. Ισχύει

για κάθε

δ. Υπάρχει

με

ε. Ισχύει

ζ. Υπάρχει

με

η. Υπάρχει

με

Μια σύντομη αιτιολόγηση είναι επιθυμητή
...Καλημέρα

μια απάντηση στο θέμα του Γιώργη...
α. Λάθος , γιατί σύμφωνα με το Θ.Μ.Ε.Τ. θα υπάρχουν μ, Μ ώστε να ισχύει
![\mu \le f(x)\le M,\,\,x\in [2,\,4] \mu \le f(x)\le M,\,\,x\in [2,\,4]](/forum/ext/geomar/texintegr/latexrender/pictures/fdfdb66236682e20e931fc30fd9a6bb0.png)
με
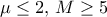
σύμφωνα με το πίνακα τιμών της

β. Λάθος, γιατί αν την ελάχιστη τιμή

και είναι

η

την παίρνει σε σημείο

θα ισχύει

που είναι άτοπο.
γ. Λάθος γιατί αν την μέγιστη τιμή

η

την παίρνει σε σημείο

τότε από Θ.Μ.Τ. και είναι

θα υπάρχει

ώστε

δ. Σωστό λόγω του Θ.Ε.Τ. αφού ισχύει ότι

ε. Αν το είναι μέγιστη τιμή της

σωστό, και αν πάλι δεν είναι μέγιστη τιμή της μπορεί

και επίσης μπορεί και

… άρα βάσει των πληροφοριών που έχουμε δεν μπορεί να δοθεί μονοσήμαντη απάντηση
ζ. Σωστό γιατί επειδή
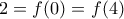
και

η

την μέγιστη τιμή την παίρνει σε σημείο

και από Fermat είναι

η. Σωστό για από Θ.Μ.Τ. στο
![[3,4] [3,4]](/forum/ext/geomar/texintegr/latexrender/pictures/b814fa889082069ffb727ee1623c0944.png)
υπάρχει

με

Φιλικά και Μαθηματικά
Βασίλης
Καλησπέρα Βασίλη, Γιώργη .
Εύχομαι σε σας και σε όλο το

καλή ακαδημαϊκή χρονιά!
Μια προσπάθεια και από μένα στην ωραία και πολύ διδακτική άσκηση του Γιώργη.
Ξεκινάμε με μια γραφική παράσταση ...

- Με πίνακα τιμών.png (27.4 KiB) Προβλήθηκε 1245 φορές
α) Λάθος , όπως φαίνεται και από την παραπάνω γραφική παράσταση .
β) Λάθος , όπως φαίνεται και από την παραπάνω γραφική παράσταση .
γ) Λάθος , διότι αν υποθέσουμε ότι
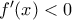


f: γνησίως φθίνουσα στο
![[2,4] [2,4]](/forum/ext/geomar/texintegr/latexrender/pictures/a157b852663a42e907fc1ae4884ff3e4.png)
,
ΑΤΟΠΟ όπως φαίνεται από την παραπάνω γραφική παράσταση .
δ) Όπως ο Βασίλης, παραπάνω.
ε) Λάθος , όπως φαίνεται και από την παραπάνω γραφική παράσταση .
ζ) Σωστό.
Από τον πίνακα τιμών ισχύει

.
Συνεπώς ισχύουν οι προϋποθέσεις του Θ.Rolle για την

στο
![[0,4] [0,4]](/forum/ext/geomar/texintegr/latexrender/pictures/b839c0a45fd15dac69be08a4dbb0b7e3.png)
.
Άρα υπάρχει τουλάχιστον ένα

τέτοιο ώστε

.
η) Σωστό.
Θεωρώ την συνάρτηση
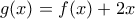
, παραγωγίσιμη με

.
Είναι

και

.
Συνεπώς ισχύουν οι προϋποθέσεις του Θ.Rolle για την

στο
![[3,4] [3,4]](/forum/ext/geomar/texintegr/latexrender/pictures/b814fa889082069ffb727ee1623c0944.png)
.
Άρα υπάρχει τουλάχιστον ένα

τέτοιο ώστε


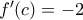
.
Φιλικά
Σταμ. Γλάρος
![\displaystyle{[0,4]} \displaystyle{[0,4]}](/forum/ext/geomar/texintegr/latexrender/pictures/c61be56947799f444c9605b715f7960c.png) Ο πίνακας αυτός εγγυάται ότι : (Σωστό ή Λάθος ; )
Ο πίνακας αυτός εγγυάται ότι : (Σωστό ή Λάθος ; )![\displaystyle{[2,5]} \displaystyle{[2,5]}](/forum/ext/geomar/texintegr/latexrender/pictures/4a861a2397252bbd9297dc495ebeccd9.png)
![\displaystyle{[0,2]} \displaystyle{[0,2]}](/forum/ext/geomar/texintegr/latexrender/pictures/ea285087bce84082ad9b0ee271285211.png)
 για κάθε
για κάθε 
 με
με 

 με
με 
 με
με 

![\mu \le f(x)\le M,\,\,x\in [2,\,4] \mu \le f(x)\le M,\,\,x\in [2,\,4]](/forum/ext/geomar/texintegr/latexrender/pictures/fdfdb66236682e20e931fc30fd9a6bb0.png) με
με 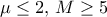 σύμφωνα με το πίνακα τιμών της
σύμφωνα με το πίνακα τιμών της 
 και είναι
και είναι  η
η  θα ισχύει
θα ισχύει  που είναι άτοπο.
που είναι άτοπο. η
η  τότε από Θ.Μ.Τ. και είναι
τότε από Θ.Μ.Τ. και είναι  θα υπάρχει
θα υπάρχει  ώστε
ώστε 

 … άρα βάσει των πληροφοριών που έχουμε δεν μπορεί να δοθεί μονοσήμαντη απάντηση
… άρα βάσει των πληροφοριών που έχουμε δεν μπορεί να δοθεί μονοσήμαντη απάντηση και
και  η
η ![[3,4] [3,4]](/forum/ext/geomar/texintegr/latexrender/pictures/b814fa889082069ffb727ee1623c0944.png) υπάρχει
υπάρχει 
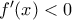

 f: γνησίως φθίνουσα στο
f: γνησίως φθίνουσα στο ![[2,4] [2,4]](/forum/ext/geomar/texintegr/latexrender/pictures/a157b852663a42e907fc1ae4884ff3e4.png) ,
, .
.![[0,4] [0,4]](/forum/ext/geomar/texintegr/latexrender/pictures/b839c0a45fd15dac69be08a4dbb0b7e3.png) .
. τέτοιο ώστε
τέτοιο ώστε  .
.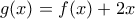 , παραγωγίσιμη με
, παραγωγίσιμη με  .
. και
και  .
. στο
στο  τέτοιο ώστε
τέτοιο ώστε 

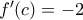 .
.
