exdx έγραψε: ↑Κυρ Ιαν 21, 2018 1:04 pm
Δίνεται η παραγωγίσιμη συνάρτηση

για τη οποία ισχύει

, για κάθε

.
Δίνεται ότι η ευθεία με εξίσωση

εφάπτεται της

σε κάποιο σημείο της , έστω
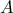
.
Α. Να προσδιορίσετε τον τύπο της
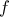
και το
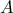
.
Β. Αν η συνάρτηση έχει τύπο

,

, τότε :
α. Να αποδείξετε ότι κάθε ευθεία που διέρχεται από τα σημεία

εφάπτεται της

στο
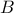
.
β. Ένα σημείο

με
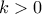
κινείται πάνω στη

και η τετμημένη του απομακρύνεται από τον

με ταχύτητα

.
Να βρείτε το ρυθμό μεταβολής της γωνίας που σχηματίζει με τον
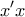
η εφαπτομένη ευθεία της

στο

, τη στιγμή που το

περνά από το
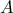
.
γ. Να βρείτε το εμβαδόν του χωρίου με σύνορα τη

και την ευθεία με εξίσωση

...Καλησπέρα

και γειά σου Γιώργη και καλή χρονιά...ένα απλό μαγειρευμα...
ΛΥΣΗ
Α. Είναι

για κάθε

και ισοδύναμα
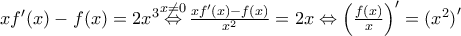
ή

(1)
Αφού η

εφάπτεται της

σε κάποιο σημείο της , έστω

θα ισχύει ότι

και

και τότε στην αρχική ισότητα θα ισχύει ότι
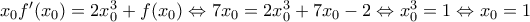
έτσι είναι

άρα

και από (1)

και έτσι από (1)

(2)
Ακόμη από

με όπου

το

προκύπτει ότι
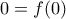
και λόγω παραγωγισιμότητας της

στο

θα είναι

και από (2)

ή

ή

επομένως από (2)

και επειδή

είναι

Β. α) Η ευθεία που διέρχεται από τα σημεία

έχει κλίση

για

αφού

και η κλίση της

στο σημείο

είναι

επομένως

άρα η ευθεία

είναι εφαπτομένη της της

στο
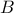
.
β) Είναι από υπόθεση

και αν
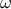
η γωνία που σχηματίζει η εφαπτομένη της

κάθε στιγμή ισχύει ότι
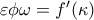
και επειδή μεταβάλλονται συναρτήσει του χρόνου ισχύει ότι

οπότε παραγωγίζοντας έχουμε ότι

και αφού

είναι

και την στιγμή που

είναι
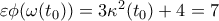
και

γ) Τα κοινά σημεία της

και της εφαπτομένης της

προκύπτουν από την επίλυση της εξίσωσης

που με σχήμα Horner γίνεται

επομένως έχουν κοινά σημεία το

σημείο επαφής και το

και έτσι το ζητούμενο εμβαδό είναι


![=\int\limits_{-2}^{1}{({{x}^{3}}-3x+2)dx}=\left[ \frac{{{x}^{4}}}{4}-3\frac{{{x}^{2}}}{2}+2x \right]_{-2}^{1}=... =\int\limits_{-2}^{1}{({{x}^{3}}-3x+2)dx}=\left[ \frac{{{x}^{4}}}{4}-3\frac{{{x}^{2}}}{2}+2x \right]_{-2}^{1}=...](/forum/ext/geomar/texintegr/latexrender/pictures/d91481119d1908e20de0f84d787c93cf.png)
Φιλικά και Μαθηματικά
Βασίλης
 για τη οποία ισχύει
για τη οποία ισχύει  , για κάθε
, για κάθε  .
.  εφάπτεται της
εφάπτεται της  σε κάποιο σημείο της , έστω
σε κάποιο σημείο της , έστω 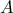 .
.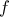 και το
και το 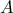 .
. ,
,  , τότε :
, τότε : εφάπτεται της
εφάπτεται της  στο
στο 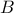 .
. με
με 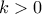 κινείται πάνω στη
κινείται πάνω στη  και η τετμημένη του απομακρύνεται από τον
και η τετμημένη του απομακρύνεται από τον  με ταχύτητα
με ταχύτητα  .
.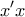 η εφαπτομένη ευθεία της
η εφαπτομένη ευθεία της  στο
στο  , τη στιγμή που το
, τη στιγμή που το  περνά από το
περνά από το 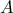 .
. και την ευθεία με εξίσωση
και την ευθεία με εξίσωση 

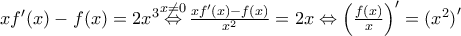 ή
ή  (1)
(1) θα ισχύει ότι
θα ισχύει ότι  και
και  και τότε στην αρχική ισότητα θα ισχύει ότι
και τότε στην αρχική ισότητα θα ισχύει ότι 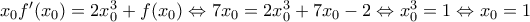
 άρα
άρα  και από (1)
και από (1)  και έτσι από (1)
και έτσι από (1)  (2)
(2)  το
το  προκύπτει ότι
προκύπτει ότι 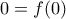 και λόγω παραγωγισιμότητας της
και λόγω παραγωγισιμότητας της  στο
στο  και από (2)
και από (2)  ή
ή  ή
ή  επομένως από (2)
επομένως από (2) και επειδή
και επειδή είναι
είναι 
 για
για  αφού
αφού  και η κλίση της
και η κλίση της  είναι
είναι  επομένως
επομένως  άρα η ευθεία
άρα η ευθεία  είναι εφαπτομένη της της
είναι εφαπτομένη της της  και αν
και αν 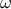 η γωνία που σχηματίζει η εφαπτομένη της
η γωνία που σχηματίζει η εφαπτομένη της 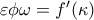 και επειδή μεταβάλλονται συναρτήσει του χρόνου ισχύει ότι
και επειδή μεταβάλλονται συναρτήσει του χρόνου ισχύει ότι  οπότε παραγωγίζοντας έχουμε ότι
οπότε παραγωγίζοντας έχουμε ότι  και αφού
και αφού  και την στιγμή που
και την στιγμή που  είναι
είναι 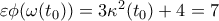 και
και 
 που με σχήμα Horner γίνεται
που με σχήμα Horner γίνεται  επομένως έχουν κοινά σημεία το
επομένως έχουν κοινά σημεία το  και έτσι το ζητούμενο εμβαδό είναι
και έτσι το ζητούμενο εμβαδό είναι 

![=\int\limits_{-2}^{1}{({{x}^{3}}-3x+2)dx}=\left[ \frac{{{x}^{4}}}{4}-3\frac{{{x}^{2}}}{2}+2x \right]_{-2}^{1}=... =\int\limits_{-2}^{1}{({{x}^{3}}-3x+2)dx}=\left[ \frac{{{x}^{4}}}{4}-3\frac{{{x}^{2}}}{2}+2x \right]_{-2}^{1}=...](/forum/ext/geomar/texintegr/latexrender/pictures/d91481119d1908e20de0f84d787c93cf.png)