 , έχει μεταβλητές τις κάθετες πλευρές αλλά η υποτείνουσά του είναι πάντα
, έχει μεταβλητές τις κάθετες πλευρές αλλά η υποτείνουσά του είναι πάντα  .
.Φέραμε την διάμεσο
 και τη διχοτόμο
και τη διχοτόμο  . Βρείτε μια συνάρτηση , η οποία να αποδίδει το
. Βρείτε μια συνάρτηση , η οποία να αποδίδει το 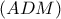 .
.Προτιμήστε ο τύπος της συνάρτησης να μην έχει ριζικό στον παρονομαστή . Πότε έχουμε :
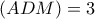 ;
;Εξηγήστε γιατί αυτό το εμβαδόν θα λάβει κάποτε μέγιστη τιμή .
Προαιρετικό : Χρησιμοποιήστε το λογισμικό σας για να βρείτε αυτή τη μέγιστη τιμή .

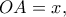 τότε
τότε 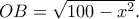 Είναι,
Είναι, 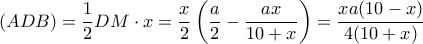
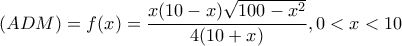
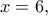 τότε
τότε 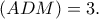 Υπάρχει άλλη μία τιμή του
Υπάρχει άλλη μία τιμή του  που δίνει εμβαδόν
που δίνει εμβαδόν  αλλά δεν μπορώ να τη βρω "δια χειρός".
αλλά δεν μπορώ να τη βρω "δια χειρός".  Προσεγγιστικά είναι
Προσεγγιστικά είναι 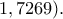
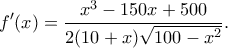 O αριθμητής έχει μία ακέραια ρίζα το
O αριθμητής έχει μία ακέραια ρίζα το 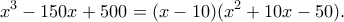 Από εδώ αφού
Από εδώ αφού 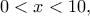 βρίσκω ότι η
βρίσκω ότι η 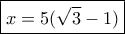 μέγιστο ίσο με
μέγιστο ίσο με 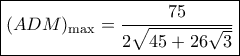
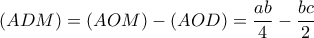 , με
, με  (*)
(*)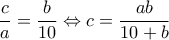
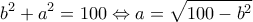
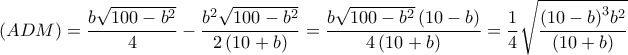
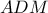 γίνεται μέγιστο όταν η συνάρτηση
γίνεται μέγιστο όταν η συνάρτηση 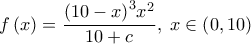 έχει μέγιστο.
έχει μέγιστο.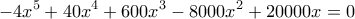

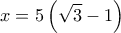 . Οι άλλες είναι
. Οι άλλες είναι 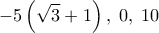 διπλή ρίζα.
διπλή ρίζα.