Ανισότητα
Συντονιστής: Καρδαμίτσης Σπύρος
-
orestisgotsis
- Δημοσιεύσεις: 1753
- Εγγραφή: Σάβ Φεβ 25, 2012 10:19 pm
Ανισότητα
ΠΕΡΙΤΤΑ
τελευταία επεξεργασία από orestisgotsis σε Παρ Φεβ 23, 2024 12:40 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Λέξεις Κλειδιά:
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3352
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ανισότητα
Ορέστη πολύ θα ήθελα να το δω και με το Διωνυμικό Θεώρημα, αλλά, μια και το έβαλες εδώ στην Γ' Λυκείου ... let's play safe (ας μην πάρουμε ρίσκα) ... και ας το δούμε με μελέτη της συνάρτησης
 ... για την οποία αρκεί να δείξουμε ότι είναι αύξουσα ... καθώς
... για την οποία αρκεί να δείξουμε ότι είναι αύξουσα ... καθώς 
Ισχύει η
![[ln(f(x))]'=\dfrac{6x}{9x^2-1}+ln\left(\dfrac{3x-1}{3x+1}\right). [ln(f(x))]'=\dfrac{6x}{9x^2-1}+ln\left(\dfrac{3x-1}{3x+1}\right).](/forum/ext/geomar/texintegr/latexrender/pictures/d4b493a16699af5ed1dd56c04d9df0c8.png) Θέτοντας
Θέτοντας  βλέπουμε ότι
βλέπουμε ότι  θα αρκούσε συνεπώς να δείξουμε ότι
θα αρκούσε συνεπώς να δείξουμε ότι  για
για 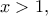 κάτι που όμως δεν ισχύει. Ισχύει όμως η
κάτι που όμως δεν ισχύει. Ισχύει όμως η  KAI επίσης η
KAI επίσης η  άρα μπορούμε να συμπεράνουμε ότι
άρα μπορούμε να συμπεράνουμε ότι  για
για 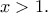
[Δεν πάει πάντως και πολύ μακριά η
 , καθώς ο λογάριθμος της τείνει στο
, καθώς ο λογάριθμος της τείνει στο  (DLH), οπότε η ίδια τείνει στο
(DLH), οπότε η ίδια τείνει στο  περίπου.]
περίπου.]Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3352
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ανισότητα
Νομίζω πως αυτή η παρατήρηση μάς δίνει και δεύτερη απόδειξη: αφού
 και
και  ... για να δείξουμε ότι η
... για να δείξουμε ότι η  δεν πέφτει κάτω από το
δεν πέφτει κάτω από το  αρκεί να δείξουμε ότι δεν μηδενίζεται η παράγωγος της (βλ. παρακάτω) -- θα είχε ένα τουλάχιστον τοπικό ελάχιστο αν έπεφτε κάτω από το
αρκεί να δείξουμε ότι δεν μηδενίζεται η παράγωγος της (βλ. παρακάτω) -- θα είχε ένα τουλάχιστον τοπικό ελάχιστο αν έπεφτε κάτω από το  αλλά ανέβαινε τελικά προς το
αλλά ανέβαινε τελικά προς το 
Βλέπουμε με λογαριθμική παραγώγιση ότι ο μηδενισμός της παραγώγου της
 είναι ισοδύναμος προς την
είναι ισοδύναμος προς την  αυτή η ισότητα είναι όμως αδύνατη για
αυτή η ισότητα είναι όμως αδύνατη για 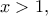 καθώς η μεν
καθώς η μεν  είναι αύξουσα η δε
είναι αύξουσα η δε  είναι φθίνουσα, και η πρώτη ήδη ξεπερνάει την δεύτερη στο
είναι φθίνουσα, και η πρώτη ήδη ξεπερνάει την δεύτερη στο 

Παραθέτω κάποιες λεπτομέρειες που χρειάστηκαν:
 ,
, 

[31-12-23 00:05 πμ] Δυστυχώς υπάρχει λάθος πρόσημο στην δεύτερη παράγωγο παραπάνω ... που ακυρώνει ολόκληρη την απόδειξη.
τελευταία επεξεργασία από gbaloglou σε Κυρ Δεκ 31, 2023 12:06 am, έχει επεξεργασθεί 1 φορά συνολικά.
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Re: Ανισότητα
Γιώργο καλημερα
για την ασκηση ΑΝΙΣΟΤΗΤΑ του διαφορικου
γινεται περίπου με διωνυμο
1) δειχνουμε οτι η ακολουθια τείνει στο
2) αρκει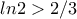
3) για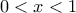 δείξε
δείξε 
4) ολοκληρωσε απο 0 ως χ
5) χ=1/2 και Ο.Κ
για την ασκηση ΑΝΙΣΟΤΗΤΑ του διαφορικου
γινεται περίπου με διωνυμο
1) δειχνουμε οτι η ακολουθια τείνει στο

2) αρκει
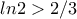
3) για
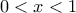 δείξε
δείξε 
4) ολοκληρωσε απο 0 ως χ
5) χ=1/2 και Ο.Κ
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3352
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ανισότητα
Ροδόλφε δεν σε πιάνω, ακολουθώντας τα παραπάνω απλώς αποδεικνύω την

Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3352
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ανισότητα
Έτσι ακριβώς, πως όμως βοηθάει αυτό στην απόδειξη της προταθείσης ανισότητας,

Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3352
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ανισότητα
Ροδόλφε ... τα παραπάνω μου θύμισαν ότι καλό είναι να δούμε την  και διωνυμικά (εκτός φακέλου βέβαια):
και διωνυμικά (εκτός φακέλου βέβαια):
Χωρίς ίσως να είναι και απαραίτητο, ας διακρίνουμε δύο περιπτώσεις,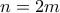 και
και 
Στην πρώτη περίπτωση, η ανισότητα γράφεται ισοδύναμα:
η ανισότητα γράφεται ισοδύναμα:


Βλέπουμε ότι ισχύει, όρο προς όρο, για η ανισότητα
η ανισότητα  , ισοδύναμη προς την
, ισοδύναμη προς την  ισχύει λοιπόν η ζητούμενη διωνυμική ανισότητα για
ισχύει λοιπόν η ζητούμενη διωνυμική ανισότητα για  και μάλιστα ως αυστηρή λόγω, αν μη τι άλλο, του 'ορφανού' τελευταίου όρου (
και μάλιστα ως αυστηρή λόγω, αν μη τι άλλο, του 'ορφανού' τελευταίου όρου ( ).
).
Στην δεύτερη περίπτωση, η απόδειξη δεν αλλάζει σχεδόν καθόλου, απλώς θα έχουμε -- ύστερα από τις αναγκαίες μεταφορές όρων --
η απόδειξη δεν αλλάζει σχεδόν καθόλου, απλώς θα έχουμε -- ύστερα από τις αναγκαίες μεταφορές όρων --  όρους στο αριστερό σκέλος και
όρους στο αριστερό σκέλος και  όρους στο δεξιό σκέλος (αντί
όρους στο δεξιό σκέλος (αντί  όρων στο αριστερό σκέλος και
όρων στο αριστερό σκέλος και  όρων στο δεξιό σκέλος της περίπτωσης
όρων στο δεξιό σκέλος της περίπτωσης 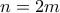 ), και η τελευταία ανισότητα θα είναι η
), και η τελευταία ανισότητα θα είναι η  ισχύουσα ως ισότητα για
ισχύουσα ως ισότητα για 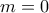
 , τότε δηλαδή που πρώτη και τελευταία ανισότητα ταυτίζονται.
, τότε δηλαδή που πρώτη και τελευταία ανισότητα ταυτίζονται.
Βλέπουμε δηλαδή ότι και στις δύο περιπτώσεις ( άρτιος και
άρτιος και  περιττός) όλα προκύπτουν από την βασική (και πανεύκολη) ανισότητα
περιττός) όλα προκύπτουν από την βασική (και πανεύκολη) ανισότητα

την οποία απλά εφαρμόζουμε για όταν
όταν 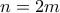 και για
και για  όταν
όταν 
[Εκτός φακέλου βγήκαμε, έχουμε όμως ένα ωραίο παράδειγμα ανισότητας που μπορεί να αποδειχθεί με δύο ριζικά διαφορετικές μεθόδους! (Δεν ήμουν και πολύ αισιόδοξος για την διωνυμική μέθοδο από την στιγμή που το όριο ( ) είναι τόσο κοντά στο
) είναι τόσο κοντά στο  , στην πραγματικότητα όμως εφαρμόζεται εύκολα ακριβώς επειδή η διαφορά των δύο ποσοτήτων είναι τεράστια (ενώ ο λόγος τους ανάμεσα στο
, στην πραγματικότητα όμως εφαρμόζεται εύκολα ακριβώς επειδή η διαφορά των δύο ποσοτήτων είναι τεράστια (ενώ ο λόγος τους ανάμεσα στο  και στο
και στο  περίπου).)]
περίπου).)]
 και διωνυμικά (εκτός φακέλου βέβαια):
και διωνυμικά (εκτός φακέλου βέβαια):Χωρίς ίσως να είναι και απαραίτητο, ας διακρίνουμε δύο περιπτώσεις,
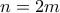 και
και 
Στην πρώτη περίπτωση,
 η ανισότητα γράφεται ισοδύναμα:
η ανισότητα γράφεται ισοδύναμα:

Βλέπουμε ότι ισχύει, όρο προς όρο, για
 η ανισότητα
η ανισότητα  , ισοδύναμη προς την
, ισοδύναμη προς την  ισχύει λοιπόν η ζητούμενη διωνυμική ανισότητα για
ισχύει λοιπόν η ζητούμενη διωνυμική ανισότητα για  και μάλιστα ως αυστηρή λόγω, αν μη τι άλλο, του 'ορφανού' τελευταίου όρου (
και μάλιστα ως αυστηρή λόγω, αν μη τι άλλο, του 'ορφανού' τελευταίου όρου ( ).
).Στην δεύτερη περίπτωση,
 η απόδειξη δεν αλλάζει σχεδόν καθόλου, απλώς θα έχουμε -- ύστερα από τις αναγκαίες μεταφορές όρων --
η απόδειξη δεν αλλάζει σχεδόν καθόλου, απλώς θα έχουμε -- ύστερα από τις αναγκαίες μεταφορές όρων --  όρους στο αριστερό σκέλος και
όρους στο αριστερό σκέλος και  όρους στο δεξιό σκέλος (αντί
όρους στο δεξιό σκέλος (αντί  όρων στο αριστερό σκέλος και
όρων στο αριστερό σκέλος και  όρων στο δεξιό σκέλος της περίπτωσης
όρων στο δεξιό σκέλος της περίπτωσης 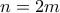 ), και η τελευταία ανισότητα θα είναι η
), και η τελευταία ανισότητα θα είναι η  ισχύουσα ως ισότητα για
ισχύουσα ως ισότητα για 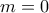
 , τότε δηλαδή που πρώτη και τελευταία ανισότητα ταυτίζονται.
, τότε δηλαδή που πρώτη και τελευταία ανισότητα ταυτίζονται.Βλέπουμε δηλαδή ότι και στις δύο περιπτώσεις (
 άρτιος και
άρτιος και  περιττός) όλα προκύπτουν από την βασική (και πανεύκολη) ανισότητα
περιττός) όλα προκύπτουν από την βασική (και πανεύκολη) ανισότητα
την οποία απλά εφαρμόζουμε για
 όταν
όταν 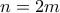 και για
και για  όταν
όταν 
[Εκτός φακέλου βγήκαμε, έχουμε όμως ένα ωραίο παράδειγμα ανισότητας που μπορεί να αποδειχθεί με δύο ριζικά διαφορετικές μεθόδους! (Δεν ήμουν και πολύ αισιόδοξος για την διωνυμική μέθοδο από την στιγμή που το όριο (
 ) είναι τόσο κοντά στο
) είναι τόσο κοντά στο  , στην πραγματικότητα όμως εφαρμόζεται εύκολα ακριβώς επειδή η διαφορά των δύο ποσοτήτων είναι τεράστια (ενώ ο λόγος τους ανάμεσα στο
, στην πραγματικότητα όμως εφαρμόζεται εύκολα ακριβώς επειδή η διαφορά των δύο ποσοτήτων είναι τεράστια (ενώ ο λόγος τους ανάμεσα στο  και στο
και στο  περίπου).)]
περίπου).)]Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3352
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ανισότητα
Τώρα που το ξαναβλέπω ... εντάξει είμαστε, είχε μπει και ένα 2 ως παρονομαστής και έτσι έβγαζα
 αντί
αντί 
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3352
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Ανισότητα
Διορθώνοντας την
 σε
σε  παρατηρώ ότι τα (3)-(5) χρησιμοποιούνται απλώς για μία 'αυτοδύναμη' απόδειξη του (2), το οποίο (2) μας δείχνει, μαζί με το (1), ότι η συνάρτηση
παρατηρώ ότι τα (3)-(5) χρησιμοποιούνται απλώς για μία 'αυτοδύναμη' απόδειξη του (2), το οποίο (2) μας δείχνει, μαζί με το (1), ότι η συνάρτηση  τείνει προς μία τιμή μεγαλύτερη του
τείνει προς μία τιμή μεγαλύτερη του  αυτό όμως δεν δίνει απόδειξη του ζητούμενου, καθώς η συνάρτηση μπορεί να ξεκινάει στο
αυτό όμως δεν δίνει απόδειξη του ζητούμενου, καθώς η συνάρτηση μπορεί να ξεκινάει στο  να πέφτει χαμηλότερα από αυτό για λίγο και αργότερα να ξανασηκώνεται για να πλησιάσει στο όριο
να πέφτει χαμηλότερα από αυτό για λίγο και αργότερα να ξανασηκώνεται για να πλησιάσει στο όριο  -- για πλήρη απόδειξη οφείλουμε να αποδείξουμε ότι είναι αύξουσα η
-- για πλήρη απόδειξη οφείλουμε να αποδείξουμε ότι είναι αύξουσα η  (ή έστω ο λογάριθμος της), κάτι που έχει γίνει στην #2.
(ή έστω ο λογάριθμος της), κάτι που έχει γίνει στην #2.Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης

 , ισχύει:
, ισχύει:  .
.
 αρα
αρα  η
η