 ισχύει
ισχύει 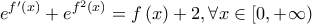 και
και  .
.Να βρεθεί ο τύπος της
 .
.Ν.Ζ.
Συντονιστής: Μπάμπης Στεργίου
Ωραία έμπνευσηnikoszan έγραψε:Για την παραγωγίσιμη συνάρτησηισχύει (1)
και
.
Να βρεθεί ο τύπος της.
Ν.Ζ.
 και
και  , άρα η (1) γίνεται
, άρα η (1) γίνεται 
 είναι φθίνουσα στο
είναι φθίνουσα στο 

 (2) θα έχουμε
(2) θα έχουμε  .
.  παραγωγίζεται δύο φορές στο
παραγωγίζεται δύο φορές στο  .
. και επειδή
και επειδή  θα έχουμε
θα έχουμε , άρα η
, άρα η  είναι κοίλη (όχι κατ΄ανάγκη γνησίως).
είναι κοίλη (όχι κατ΄ανάγκη γνησίως). έχουμε
έχουμε  , τότε από την κοιλότητα έχουμε:
, τότε από την κοιλότητα έχουμε: και επειδή
και επειδή ![\displaystyle{\lim_{x \to +\infty}\left[f'(x_0)(x-x_0)+f(x_0)\right]=-\infty} \displaystyle{\lim_{x \to +\infty}\left[f'(x_0)(x-x_0)+f(x_0)\right]=-\infty}](/forum/ext/geomar/texintegr/latexrender/pictures/63927d6ef6a724f6d7f365200b3e0e1e.png)
 , το οποίο είναι αντίφαση, γιατί η (1) δίνει
, το οποίο είναι αντίφαση, γιατί η (1) δίνει  .
. και η (2) δίνει
και η (2) δίνει  , που επαληθεύει τα δεδομένα.
, που επαληθεύει τα δεδομένα.


 επαληθεύει το πρόβλημα.Αν χρησιμοποιήσουμε το θεώρημα μοναδικότητας-ύπαρξης
επαληθεύει το πρόβλημα.Αν χρησιμοποιήσουμε το θεώρημα μοναδικότητας-ύπαρξης μια συνεχής συνάρτηση που ορίζεται γύρω από το
μια συνεχής συνάρτηση που ορίζεται γύρω από το 
 και η
και η  υπάρχει.
υπάρχει.

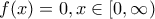

 είναι συνεχής και
είναι συνεχής και 

 είναι συνεχής έχει παράγουσα.
είναι συνεχής έχει παράγουσα.



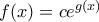
 προκύπτει
προκύπτει  οπότε
οπότε 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες