 για την οποία ισχύουν
για την οποία ισχύουν  και
και  .
.Ν.Ζ.
Συντονιστής: Μπάμπης Στεργίου
 για την οποία ισχύουν
για την οποία ισχύουν  και
και  .
.
 αρχική της
αρχική της  με
με 

 \displaystyle{\displaystyle{
\displaystyle{\displaystyle{ \displaystyle{
\displaystyle{ \displaystyle{
\displaystyle{ \displaystyle{
\displaystyle{





 που επαληθεύει τα δεδομένα.
που επαληθεύει τα δεδομένα.
![\Rightarrow \left. {\begin{array}{*{20}{c}}
{{{\left( {1 - f\left( x \right)} \right)}^\prime } + \left( {1 - f\left( x \right)} \right)\left( {1 + f\left( x \right)} \right) = 0}\\
{{{\left( {1 + f\left( x \right)} \right)}^\prime } - \left( {1 - f\left( x \right)} \right)\left( {1 + f\left( x \right)} \right) = 0}
\end{array}} \right\} \Rightarrow \left. {\begin{array}{*{20}{c}}
{{{\left[ {\left( {1 - f\left( x \right)} \right){e^{\int\limits_0^x {\left( {1 + f\left( t \right)} \right)dt} }}} \right]}^\prime } = 0}\\
{{{\left[ {\left( {1 + f\left( x \right)} \right){e^{ - \int\limits_0^x {\left( {1 - f\left( t \right)} \right)dt} }}} \right]}^\prime } = 0}
\end{array}} \right\} \Rightarrow \Rightarrow \left. {\begin{array}{*{20}{c}}
{{{\left( {1 - f\left( x \right)} \right)}^\prime } + \left( {1 - f\left( x \right)} \right)\left( {1 + f\left( x \right)} \right) = 0}\\
{{{\left( {1 + f\left( x \right)} \right)}^\prime } - \left( {1 - f\left( x \right)} \right)\left( {1 + f\left( x \right)} \right) = 0}
\end{array}} \right\} \Rightarrow \left. {\begin{array}{*{20}{c}}
{{{\left[ {\left( {1 - f\left( x \right)} \right){e^{\int\limits_0^x {\left( {1 + f\left( t \right)} \right)dt} }}} \right]}^\prime } = 0}\\
{{{\left[ {\left( {1 + f\left( x \right)} \right){e^{ - \int\limits_0^x {\left( {1 - f\left( t \right)} \right)dt} }}} \right]}^\prime } = 0}
\end{array}} \right\} \Rightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/aae8234b810b7e6081feb1281a4aae72.png)


 .
.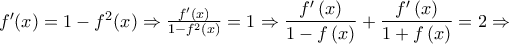

 .
. μετασχηματίζεται στην
μετασχηματίζεται στην 

 είναι
είναι  και έτσι
και έτσι 
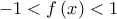 είναι ο παρακάτω:
είναι ο παρακάτω:
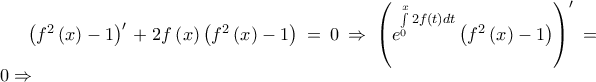


 δηλαδή
δηλαδή 




 οπότε
οπότε 


 όταν
όταν  πράγμα που εδώ δεν ισχύει. Αυτό παρακάμπτεται με τον περιορισμό του προβλήματος στα διαστήματα όπου εννοείται ότι είναι
πράγμα που εδώ δεν ισχύει. Αυτό παρακάμπτεται με τον περιορισμό του προβλήματος στα διαστήματα όπου εννοείται ότι είναι  . Προκύπτουν λοιπόν όπως μπορούμε να δούμε και από τον τρόπο γραφής και οι λύσεις
. Προκύπτουν λοιπόν όπως μπορούμε να δούμε και από τον τρόπο γραφής και οι λύσεις  και
και 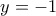 οι οποίες απορρίπτονται ως μη διερχόμενες από το μηδέν. Απομένει λοιπόν μια λύση για όλο το R. Ευχαριστώ.
οι οποίες απορρίπτονται ως μη διερχόμενες από το μηδέν. Απομένει λοιπόν μια λύση για όλο το R. Ευχαριστώ.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Αγαπητέ Κώστα χαίρομαι που συμμετέχεις στις συζητήσεις.
Εδώ διαίρεσα χωρίς να υποθέσω ότι δεν μηδενίζεται.
Οταν πάμε να λύσουμε μια διαφορική εξίσωση η μια εξίσωση δεν κοιτάμε τους περιορισμούς.
Προσπαθούμε να βρούμε την λύση.Αφου την βρούμε κοιτάμε αν όλα έχουν γίνει σωστά.
Αυτή είναι η άποψη μου, που αποκόμισα από τους δασκάλους μου.
Γνωρίζω ότι υπάρχουν και άλλες απόψεις.
Στο συγκεκριμένο θέμα έγραψα αυτή την λύση για να δείξω ότι δεν χρειάζονται τα ακροβατικά
που είχαν κάνει οι προηγούμενοι.
Δυστυχώς αν κάτι είναι ακροβατικό θεωρείται εντός ύλης ενώ αν χρησιμοποιείτε κάτι που δεν είναι σαφώς
γραμμένο είναι εκτός ύλης.
Και μετά ψάχνουν οι έχοντες την αντίθετη άποψη γιατί έχουν καταντήσει έτσι τα σχολικά μαθηματικά.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες