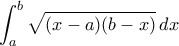 ,
,όπου
 .
.Συντονιστής: Μπάμπης Στεργίου
![\begin{array}{l}
I = \int\limits_\alpha ^\beta {\sqrt {\left( {x - \alpha } \right)\left( {x - \beta } \right)} } dx = \frac{{\left| {\alpha - \beta } \right|}}{2}\int\limits_\alpha ^\beta {\sqrt {1 - {{\left( {\frac{{x - \frac{{\alpha + \beta }}{2}}}{{\frac{{\alpha - \beta }}{2}}}} \right)}^2}} } dx\mathop = \limits_{dx = \frac{{\alpha - \beta }}{2}\sigma \upsilon \nu tdt}^{\frac{{x - \frac{{\alpha + \beta }}{2}}}{{\frac{{\alpha - \beta }}{2}}} = \eta \mu t} \\
= - \frac{{\left| {\alpha - \beta } \right|}}{2}\int\limits_{ - \frac{\pi }{2}}^{\frac{\pi }{2}} {\frac{{\alpha - \beta }}{2}\sigma \upsilon {\nu ^2}tdt} = - \frac{{\left| {\alpha - \beta } \right|\left( {\alpha - \beta } \right)}}{4}\left[ {\frac{t}{2} + \frac{{\eta \mu 2t}}{4}} \right]_{ - \frac{\pi }{2}}^{\frac{\pi }{2}} = \\
= - \frac{{\left| {\alpha - \beta } \right|\left( {\alpha - \beta } \right)\pi }}{8} \\
\end{array} \begin{array}{l}
I = \int\limits_\alpha ^\beta {\sqrt {\left( {x - \alpha } \right)\left( {x - \beta } \right)} } dx = \frac{{\left| {\alpha - \beta } \right|}}{2}\int\limits_\alpha ^\beta {\sqrt {1 - {{\left( {\frac{{x - \frac{{\alpha + \beta }}{2}}}{{\frac{{\alpha - \beta }}{2}}}} \right)}^2}} } dx\mathop = \limits_{dx = \frac{{\alpha - \beta }}{2}\sigma \upsilon \nu tdt}^{\frac{{x - \frac{{\alpha + \beta }}{2}}}{{\frac{{\alpha - \beta }}{2}}} = \eta \mu t} \\
= - \frac{{\left| {\alpha - \beta } \right|}}{2}\int\limits_{ - \frac{\pi }{2}}^{\frac{\pi }{2}} {\frac{{\alpha - \beta }}{2}\sigma \upsilon {\nu ^2}tdt} = - \frac{{\left| {\alpha - \beta } \right|\left( {\alpha - \beta } \right)}}{4}\left[ {\frac{t}{2} + \frac{{\eta \mu 2t}}{4}} \right]_{ - \frac{\pi }{2}}^{\frac{\pi }{2}} = \\
= - \frac{{\left| {\alpha - \beta } \right|\left( {\alpha - \beta } \right)\pi }}{8} \\
\end{array}](/forum/ext/geomar/texintegr/latexrender/pictures/082a4984a0e725de9b6544311de8bc0a.png)
Ωραίος. Υπάρχει και κάποια άλλη αντικατάσταση που δουλεύει αλλά δεν τη βάζω πρίν να λυθεί και αυτή.mathxl έγραψε:Μία λύση
 τοτε το ολοκληρωμα ισουται με
τοτε το ολοκληρωμα ισουται με  οπου c είναι η διαφορά της αριθμητικής προόδου α, (α+b)/2, b κατόπιν αν θέσουμε ξανά
οπου c είναι η διαφορά της αριθμητικής προόδου α, (α+b)/2, b κατόπιν αν θέσουμε ξανά 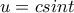
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες