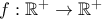 είναι τέτοια ώστε
είναι τέτοια ώστε  για κάθε
για κάθε 
Να δείξετε ότι είναι 1-1.
Μπορούμε να βρούμε τις συναρτήσεις με αυτή την ιδιότητα;
Συντονιστής: Μπάμπης Στεργίου
 Τότε για
Τότε για  παίρνω
παίρνω 
 Aν
Aν  και επειδή η
και επειδή η  είναι και ΕΠΙ λόγω της
είναι και ΕΠΙ λόγω της  έπεται ότι
έπεται ότι 
 Θέτοντας
Θέτοντας  προκύπτουν
προκύπτουν από το πεδίο ορισμού και το σύνολο άφιξης της
από το πεδίο ορισμού και το σύνολο άφιξης της 
 με
με 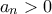 οπότε
οπότε  συνεπως
συνεπως  δηλαδή
δηλαδή  oi ανισότητες αυτές εξασφαλίζουν οτι
oi ανισότητες αυτές εξασφαλίζουν οτι 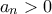
 οποιοσδήποτε θετικός,
οποιοσδήποτε θετικός,  οποιοσδήποτε θετικός και σκέφτηκα ότι οποιοσδήποτε θετικός+οποιοσδήποτε θετικός=οποιοσδήποτε θετικός αρα
οποιοσδήποτε θετικός και σκέφτηκα ότι οποιοσδήποτε θετικός+οποιοσδήποτε θετικός=οποιοσδήποτε θετικός αρα  οποιoσδήποτε θετικός δηλαδή
οποιoσδήποτε θετικός δηλαδή  επί
επίΑυτό όμως δεν ισχύει αν π.χ.R BORIS έγραψε:αφού f επίοποιοσδήποτε θετικός,
οποιοσδήποτε θετικός και σκέφτηκα ότι οποιοσδήποτε θετικός+οποιοσδήποτε θετικός=οποιοσδήποτε θετικός αρα
οποιoσδήποτε θετικός δηλαδή
επί

 .
.Λάμπρο, αν θέλεις γράψε την απόδειξή σου ότιΛάμπρος Μπαλός έγραψε:Επαναφορά.
Μέσα στο χάος των χαρτιών είχα αποδείξει πως αν είναι 1-1 θα είναι η.
Το 1-1 όμως δεν το απέδειξα. Θα ξαναπροσπαθήσω, αν δεν υπάρξει απόδειξη.
 για κάθε
για κάθε  χρησιμοποιώντας το 1-1.
χρησιμοποιώντας το 1-1.  (σχέση 1)
(σχέση 1) (σχέση 2)
(σχέση 2)
 (σχέση 3)
(σχέση 3) (σχέση 4)
(σχέση 4)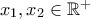 με:
με:![\mathbf{f(x_1)=f(x_2)}\Rightarrow f(f(x_1))=f(f(x_2))\xrightarrow[]{f(x_1)=f(x_2)}\newline\rightarrow f(f(x_1))+f(x_1)=f(f(x_2))+f(x_2)\overset{(4)}{\Rightarrow} 2x_1=2x_2\Rightarrow \mathbf{x_1=x_2} \mathbf{f(x_1)=f(x_2)}\Rightarrow f(f(x_1))=f(f(x_2))\xrightarrow[]{f(x_1)=f(x_2)}\newline\rightarrow f(f(x_1))+f(x_1)=f(f(x_2))+f(x_2)\overset{(4)}{\Rightarrow} 2x_1=2x_2\Rightarrow \mathbf{x_1=x_2}](/forum/ext/geomar/texintegr/latexrender/pictures/7eaabd12f4fb314c185acb83052b173b.png)
ΤοAndreas A. έγραψε:Καλησπέρα. Μια πιο "λυκειακή" προσέγγιση του θέματος:
Ισχύει:(σχέση 1)
Στην (1) θέτουμε x=y=0:
(σχέση 2)
Στην (1) μπορουμε να θέσουμε x=y=f(0), αφού από το σύνολο αφίξεως γνωρίζουμε ότι:
(1) για x=y=f(0):
(σχέση 3)
Στην (1) θέτουμε y=0:
(σχέση 4)
Τώρα έστωμε:
Άρα f:1-1
 δεν περιέχει το
δεν περιέχει το 
Το έχω συναντήσει να ορίζεται ωςΤοδεν περιέχει το
(έτσι νομίζω)
 και όταν δεν περιέχει το 0 να συμβολίζεται
και όταν δεν περιέχει το 0 να συμβολίζεται  , δηλαδή
, δηλαδή  , αλλά με μια πρόχειρη έρευνα που έκανα, τώρα που αναφέρθηκε, κατάλαβα ότι διαφέρει από συγγραφέα σε συγγραφέα το αν το
, αλλά με μια πρόχειρη έρευνα που έκανα, τώρα που αναφέρθηκε, κατάλαβα ότι διαφέρει από συγγραφέα σε συγγραφέα το αν το  περιέχει το 0 η όχι. Αξίζει λοιπόν να διευκρινιστεί αν εδώ το
περιέχει το 0 η όχι. Αξίζει λοιπόν να διευκρινιστεί αν εδώ το  εννοείται με η χωρίς το 0. Αν κάποιος γνωρίζει κάτι παραπάνω στο θέμα ας μου το διασαφηνίσει, γιατί άκρη δεν βρήκα.
εννοείται με η χωρίς το 0. Αν κάποιος γνωρίζει κάτι παραπάνω στο θέμα ας μου το διασαφηνίσει, γιατί άκρη δεν βρήκα. συγνωμη για το χονδροειδες λαθος. Μια άλλη σκεψηR BORIS έγραψε:αφού f επίοποιοσδήποτε θετικός,
οποιοσδήποτε θετικός και σκέφτηκα ότι οποιοσδήποτε θετικός+οποιοσδήποτε θετικός=οποιοσδήποτε θετικός αρα
οποιoσδήποτε θετικός δηλαδή
επί
 επι αρα
επι αρα  επι
επι το
το  αρα
αρα  επί αρα
επί αρα  επί
επίΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες