erxmer έγραψε:Δίνεται συνάρτηση
![f: [1,2] \to \mathbb{R} f: [1,2] \to \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/66cb5ffb24fdba6efffba93b3b48e9da.png)
παραγωγίσιμη, με συνεχή πρώτη παράγωγο και
![f(1)=2, f'(x)<0, x \in [1,2] f(1)=2, f'(x)<0, x \in [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/8e8451f8eb4ed30dcc6254d06409839d.png)
.
1) Να αποδείξετε οτι είναι αντιστρέψιμη και να βρεθεί το πεδίο ορισμού της αντίστροφης
Αν η

είναι συνεχής και ισχύει οτι:

2) Nα βρεθεί το

3) Yπάρχει τουλάχιστον ενα

ώστε η εφαπτομένη της

στο σημείο

είναι παράλληλη στην ευθεία

4) H

τέμνει την διχοτόμο της 1ης και της 3ης γωνίας των αξόνων σε ακριβώς ενα σημείο με τετμημένη

5)

6) Αν

τοτε

Κάπως αντίστροφα για τα πρώτα δύο ερωτήματα.
α) Προφανώς η

είναι αντιστρέψιμη αφού είναι γνησίως φθίνουσα διότι
![f'(x)<0 \; \forall x \in [1, 2] f'(x)<0 \; \forall x \in [1, 2]](/forum/ext/geomar/texintegr/latexrender/pictures/3db5757d690c1e55cf0b97ccaaff6165.png)
.
β) Από τη σχέση που δίδεται έχουμε
![\displaystyle{\begin{aligned}
\int_{f(1)}^{f(2)} f^{-1}(t) \, {\rm d}t +\int_{1}^{2}f(t) \, {\rm d}t =0 &\overset{t=f(x)}{=\! =\! =\! =\!} \int_{1}^{2} x f'(x) \, {\rm d}x + \int_{1}^{2} f(x) \, {\rm d}x =0 \\
&\Leftrightarrow \left [ x f(x) \right ]_1^2 + \cancel{\int_{1}^{2} f(x) \, {\rm d}x - \int_{1}^{2} f(x) \, {\rm d}x} =0\\
&\Leftrightarrow 2 f(2) - f(1)=0 \\
&\Leftrightarrow 2f(2) =2 \\
&\Leftrightarrow f(2)=1
\end{aligned}} \displaystyle{\begin{aligned}
\int_{f(1)}^{f(2)} f^{-1}(t) \, {\rm d}t +\int_{1}^{2}f(t) \, {\rm d}t =0 &\overset{t=f(x)}{=\! =\! =\! =\!} \int_{1}^{2} x f'(x) \, {\rm d}x + \int_{1}^{2} f(x) \, {\rm d}x =0 \\
&\Leftrightarrow \left [ x f(x) \right ]_1^2 + \cancel{\int_{1}^{2} f(x) \, {\rm d}x - \int_{1}^{2} f(x) \, {\rm d}x} =0\\
&\Leftrightarrow 2 f(2) - f(1)=0 \\
&\Leftrightarrow 2f(2) =2 \\
&\Leftrightarrow f(2)=1
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/b9fc715475fe75f07debc4b3cee70bdf.png)
άρα

. Επειδή η

είναι συνεχής και γνησίως φθίνουσα το σύνολο τιμών είναι το
![f\left ( \left [ 1, 2 \right ] \right )= \left [ f\left ( 2 \right ), f\left ( 1 \right ) \right ] = \left [ 1, 2 \right ] f\left ( \left [ 1, 2 \right ] \right )= \left [ f\left ( 2 \right ), f\left ( 1 \right ) \right ] = \left [ 1, 2 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/5d3de925443b3f6828831ffdc2ce34c8.png)
.
γ) Αρκεί να δείξουμε ότι υπάρχει

τέτοιο ώστε

. Από Θέωρημα Μέσης Τιμής για τη παραγωγίσιμη στο
![[1, 2] [1, 2]](/forum/ext/geomar/texintegr/latexrender/pictures/04cd0e0151f352e7fd414d694a604136.png)
συνάρτηση έχουμε ότι υπάρχει ένα

τέτοιο ώστε

όπως θέλαμε.
δ) Η διχοτόμος της πρώτης και τρίτης γωνίας των αξόνων δεν είναι άλλη από την ευθεία

. Θεωρώντας τη συνάρτηση

εύκολα διαπιστώνουμε ότι είναι γνήσια φθίνουσα καθώς και ότι

,

. Οπότε από θεώρημα Bolzano υπάρχει ένα τουλάχιστον

τέτοιο ώστε

το οποίο λόγω μονοτονίας είναι μοναδικό.
ε) Η

ικανοποιεί τις προϋποθέσεις του Θεωρήματος Μέσης Τιμής στα διαστήματα
![[1, x_0] [1, x_0]](/forum/ext/geomar/texintegr/latexrender/pictures/5f8829a8b5f4d4e50c90034469d1f65d.png)
και
![[x_0, 2] [x_0, 2]](/forum/ext/geomar/texintegr/latexrender/pictures/ddef5f371d7e93cf8194ce34e04bb096.png)
. Οπότε από εφαρμογή του θεωρήματος στο διάστημα
![[1, x_0] [1, x_0]](/forum/ext/geomar/texintegr/latexrender/pictures/5f8829a8b5f4d4e50c90034469d1f65d.png)
υπάρχει ένα

τέτοιο ώστε

και στο διάστημα
![[x_0, 2] [x_0, 2]](/forum/ext/geomar/texintegr/latexrender/pictures/ddef5f371d7e93cf8194ce34e04bb096.png)
υπάρχει ένα

τέτοιο ώστε

. Οπότε:
 στ) Δυστυχώς δε μπορώ να βγάλω το
στ) Δυστυχώς δε μπορώ να βγάλω το  ως το φράγμα που δίδει η άσκηση. Βγάζω
ως το φράγμα που δίδει η άσκηση. Βγάζω  . Αυτό που έκανα είναι το εξής:
. Αυτό που έκανα είναι το εξής: Από το σύνολο τιμών γνωρίζουμε ότι

. Άρα

. Με πρόσθεση κατά μέλη έχουμε διαδοχικά:


 Τι δε βλέπω;
Τι δε βλέπω;![f: [1,2] \to \mathbb{R} f: [1,2] \to \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/66cb5ffb24fdba6efffba93b3b48e9da.png) παραγωγίσιμη, με συνεχή πρώτη παράγωγο και
παραγωγίσιμη, με συνεχή πρώτη παράγωγο και ![f(1)=2, f'(x)<0, x \in [1,2] f(1)=2, f'(x)<0, x \in [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/8e8451f8eb4ed30dcc6254d06409839d.png) .
. είναι συνεχής και ισχύει οτι:
είναι συνεχής και ισχύει οτι:

 ώστε η εφαπτομένη της
ώστε η εφαπτομένη της  στο σημείο
στο σημείο  είναι παράλληλη στην ευθεία
είναι παράλληλη στην ευθεία 
 τέμνει την διχοτόμο της 1ης και της 3ης γωνίας των αξόνων σε ακριβώς ενα σημείο με τετμημένη
τέμνει την διχοτόμο της 1ης και της 3ης γωνίας των αξόνων σε ακριβώς ενα σημείο με τετμημένη 

 τοτε
τοτε 

 είναι αντιστρέψιμη αφού είναι γνησίως φθίνουσα διότι
είναι αντιστρέψιμη αφού είναι γνησίως φθίνουσα διότι ![f'(x)<0 \; \forall x \in [1, 2] f'(x)<0 \; \forall x \in [1, 2]](/forum/ext/geomar/texintegr/latexrender/pictures/3db5757d690c1e55cf0b97ccaaff6165.png) .
. ![\displaystyle{\begin{aligned}
\int_{f(1)}^{f(2)} f^{-1}(t) \, {\rm d}t +\int_{1}^{2}f(t) \, {\rm d}t =0 &\overset{t=f(x)}{=\! =\! =\! =\!} \int_{1}^{2} x f'(x) \, {\rm d}x + \int_{1}^{2} f(x) \, {\rm d}x =0 \\
&\Leftrightarrow \left [ x f(x) \right ]_1^2 + \cancel{\int_{1}^{2} f(x) \, {\rm d}x - \int_{1}^{2} f(x) \, {\rm d}x} =0\\
&\Leftrightarrow 2 f(2) - f(1)=0 \\
&\Leftrightarrow 2f(2) =2 \\
&\Leftrightarrow f(2)=1
\end{aligned}} \displaystyle{\begin{aligned}
\int_{f(1)}^{f(2)} f^{-1}(t) \, {\rm d}t +\int_{1}^{2}f(t) \, {\rm d}t =0 &\overset{t=f(x)}{=\! =\! =\! =\!} \int_{1}^{2} x f'(x) \, {\rm d}x + \int_{1}^{2} f(x) \, {\rm d}x =0 \\
&\Leftrightarrow \left [ x f(x) \right ]_1^2 + \cancel{\int_{1}^{2} f(x) \, {\rm d}x - \int_{1}^{2} f(x) \, {\rm d}x} =0\\
&\Leftrightarrow 2 f(2) - f(1)=0 \\
&\Leftrightarrow 2f(2) =2 \\
&\Leftrightarrow f(2)=1
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/b9fc715475fe75f07debc4b3cee70bdf.png)
 . Επειδή η
. Επειδή η ![f\left ( \left [ 1, 2 \right ] \right )= \left [ f\left ( 2 \right ), f\left ( 1 \right ) \right ] = \left [ 1, 2 \right ] f\left ( \left [ 1, 2 \right ] \right )= \left [ f\left ( 2 \right ), f\left ( 1 \right ) \right ] = \left [ 1, 2 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/5d3de925443b3f6828831ffdc2ce34c8.png) .
. τέτοιο ώστε
τέτοιο ώστε  . Από Θέωρημα Μέσης Τιμής για τη παραγωγίσιμη στο
. Από Θέωρημα Μέσης Τιμής για τη παραγωγίσιμη στο ![[1, 2] [1, 2]](/forum/ext/geomar/texintegr/latexrender/pictures/04cd0e0151f352e7fd414d694a604136.png) συνάρτηση έχουμε ότι υπάρχει ένα
συνάρτηση έχουμε ότι υπάρχει ένα 
 . Θεωρώντας τη συνάρτηση
. Θεωρώντας τη συνάρτηση  εύκολα διαπιστώνουμε ότι είναι γνήσια φθίνουσα καθώς και ότι
εύκολα διαπιστώνουμε ότι είναι γνήσια φθίνουσα καθώς και ότι  ,
,  . Οπότε από θεώρημα Bolzano υπάρχει ένα τουλάχιστον
. Οπότε από θεώρημα Bolzano υπάρχει ένα τουλάχιστον  τέτοιο ώστε
τέτοιο ώστε  το οποίο λόγω μονοτονίας είναι μοναδικό.
το οποίο λόγω μονοτονίας είναι μοναδικό.![[1, x_0] [1, x_0]](/forum/ext/geomar/texintegr/latexrender/pictures/5f8829a8b5f4d4e50c90034469d1f65d.png) και
και ![[x_0, 2] [x_0, 2]](/forum/ext/geomar/texintegr/latexrender/pictures/ddef5f371d7e93cf8194ce34e04bb096.png) . Οπότε από εφαρμογή του θεωρήματος στο διάστημα
. Οπότε από εφαρμογή του θεωρήματος στο διάστημα  τέτοιο ώστε
τέτοιο ώστε  και στο διάστημα
και στο διάστημα  τέτοιο ώστε
τέτοιο ώστε  . Οπότε:
. Οπότε:
 ως το φράγμα που δίδει η άσκηση. Βγάζω
ως το φράγμα που δίδει η άσκηση. Βγάζω  . Αυτό που έκανα είναι το εξής: Από το σύνολο τιμών γνωρίζουμε ότι
. Αυτό που έκανα είναι το εξής: Από το σύνολο τιμών γνωρίζουμε ότι  . Άρα
. Άρα  . Με πρόσθεση κατά μέλη έχουμε διαδοχικά:
. Με πρόσθεση κατά μέλη έχουμε διαδοχικά:

![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) με
με  .
. 


 με
με  και
και  . Τότε
. Τότε  .
. . Ισχύει
. Ισχύει  .
.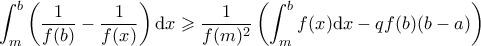 .
. με
με  . Μετα είναι θέμα πράξεων...
. Μετα είναι θέμα πράξεων...