erxmer έγραψε:Δίνεται η συνεχής συνάρτηση

στο

ώστε

1) Αποδείξτε οτι η

είναι παραγωγισιμή.
2) Ποιός είναι ο τύπος της

;
3) Υπάρχει τουλάχιστον ένα σημείο

με

ώστε η εφαπτομένη της

να σχηματίζει με τους άξονες τρίγωνο εμβαδού

μονάδες. Eπίσης να βρεθεί το

για το οποίο το εμβαδόν του τριγώνου ελαχιστοποιείται.
4)
![\displaystyle{\lim_{x \to +\infty}\left [ F(x+1)-F(x) \right ]=0} \displaystyle{\lim_{x \to +\infty}\left [ F(x+1)-F(x) \right ]=0}](/forum/ext/geomar/texintegr/latexrender/pictures/78bb1f02ade7a307a953364a2434dd50.png)
με

μια αρχική της

.
5) H εξίσωση

έχει μοναδική ρίζα
...και μετά τις επεμβάσεις του δημιουργού....
1) Είναι

με
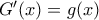
άρα η

είναι παραγωγίσιμη ως σύνθεση παραγωγίσιμων με

2) Είναι

και λόγω του

έχουμε ότι

και επειδή από

είναι

προκύπτει ότι

επομένως από

και αν

τότε

επομένως είναι

3) Θέλουμε η εφαπτομένη της , σε ένα σημείο

με

που έχει εξίσωση

και επειδή

η

που τέμνει τους άξονες στα σημεία

και σχηματίζει εμβαδό

που είναι ίσο με

δηλαδή να ισχύει

Γι αυτό θεωρούμε την συνάρτηση
![h(x)=x{{\left( 1+f(x) \right)}^{2}}-16,\,\,\,x\in [e,\,\,{{e}^{2}}] h(x)=x{{\left( 1+f(x) \right)}^{2}}-16,\,\,\,x\in [e,\,\,{{e}^{2}}]](/forum/ext/geomar/texintegr/latexrender/pictures/209bd5e43670dcce578fafbb46e67ed6.png)
που είναι συνεχής με

και

και επειδή

σύμφωνα με το θεώρημα του Bolzano υπάρχει

που

Για το ερώτημα του ελαχίστου τώρα το εμβαδό του τριγώνου δίνεται από την συνάρτηση

που είναι παραγωγίσιμη με

Για την συνάρτηση


προφανώς

και

και

αφού

έτσι για την

επειδή

ισχύει ότι

άρα η

είναι γνήσια φθίνουσα στο
![(1,\,\,e] (1,\,\,e]](/forum/ext/geomar/texintegr/latexrender/pictures/e13a1d2f4aca6ff588ae89e35c7210a3.png)
και

άρα η

είναι γνήσια αύξουσα στο

άρα παρουσιάζει ελάχιστο στο

4) Είναι στο διάστημα
![[x,\,x+1] [x,\,x+1]](/forum/ext/geomar/texintegr/latexrender/pictures/674fceaa1524379dbb18b38e604ee77a.png)
η

και σύμφωνα με το θεώρημα της μέσης τιμής υπάρχει

με

και επειδή η

είναι γνήσια φθίνουσα στο

και

άρα ισχύει ότι

και επειδή

και

από το κριτήριο παρεμβολής έχουμε ότι

...σε λίγο το (5)...
Φιλικά και Μαθηματικά
Βασίλης
 στο
στο  ώστε
ώστε 
 είναι παραγωγισιμή.
είναι παραγωγισιμή. ;
; με
με  ώστε η εφαπτομένη της
ώστε η εφαπτομένη της 
 μονάδες. Eπίσης να βρεθεί το
μονάδες. Eπίσης να βρεθεί το  για το οποίο το εμβαδόν του τριγώνου ελαχιστοποιείται.
για το οποίο το εμβαδόν του τριγώνου ελαχιστοποιείται.![\displaystyle{\lim_{x \to +\infty}\left [ F(x+1)-F(x) \right ]=0} \displaystyle{\lim_{x \to +\infty}\left [ F(x+1)-F(x) \right ]=0}](/forum/ext/geomar/texintegr/latexrender/pictures/78bb1f02ade7a307a953364a2434dd50.png) με
με  μια αρχική της
μια αρχική της  .
. έχει μοναδική ρίζα
έχει μοναδική ρίζα

 με
με 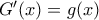 άρα η
άρα η 
 και λόγω του
και λόγω του  έχουμε ότι
έχουμε ότι  και επειδή από
και επειδή από  προκύπτει ότι
προκύπτει ότι 

 τότε
τότε  επομένως είναι
επομένως είναι 
 είναι μεγάλος . Μπορεί να ζητηθεί κάτι γύρω στο
είναι μεγάλος . Μπορεί να ζητηθεί κάτι γύρω στο 
 και επειδή
και επειδή  η
η 


 δηλαδή να ισχύει
δηλαδή να ισχύει 
![h(x)=x{{\left( 1+f(x) \right)}^{2}}-16,\,\,\,x\in [e,\,\,{{e}^{2}}] h(x)=x{{\left( 1+f(x) \right)}^{2}}-16,\,\,\,x\in [e,\,\,{{e}^{2}}]](/forum/ext/geomar/texintegr/latexrender/pictures/209bd5e43670dcce578fafbb46e67ed6.png) που είναι συνεχής με
που είναι συνεχής με και
και  και επειδή
και επειδή  σύμφωνα με το θεώρημα του Bolzano υπάρχει
σύμφωνα με το θεώρημα του Bolzano υπάρχει  που
που 
 που είναι παραγωγίσιμη με
που είναι παραγωγίσιμη με 

 προφανώς
προφανώς  και
και  και
και  αφού
αφού  έτσι για την
έτσι για την  επειδή
επειδή  ισχύει ότι
ισχύει ότι  άρα η
άρα η  είναι γνήσια φθίνουσα στο
είναι γνήσια φθίνουσα στο ![(1,\,\,e] (1,\,\,e]](/forum/ext/geomar/texintegr/latexrender/pictures/e13a1d2f4aca6ff588ae89e35c7210a3.png) και
και 
 άρα παρουσιάζει ελάχιστο στο
άρα παρουσιάζει ελάχιστο στο 
![[x,\,x+1] [x,\,x+1]](/forum/ext/geomar/texintegr/latexrender/pictures/674fceaa1524379dbb18b38e604ee77a.png) η
η  και σύμφωνα με το θεώρημα της μέσης τιμής υπάρχει
και σύμφωνα με το θεώρημα της μέσης τιμής υπάρχει  με
με  και επειδή η
και επειδή η  και
και  άρα ισχύει ότι
άρα ισχύει ότι  και επειδή
και επειδή  και
και  από το κριτήριο παρεμβολής έχουμε ότι
από το κριτήριο παρεμβολής έχουμε ότι 
 και
και 