Επειδή κάτι που έγραψα για την απόδειξη του 5) έγινε αντικείμενο κριτικής, αμφισβητήσεων και ενστάσεων (είναι αλήθεια ότι ήταν πολύ συμπυκνωμένο) χαίρομαι που μου ζητήθηκε να το ξαναγράψω αναλυτικά, διότι φαίνεται ότι δεν πέρασε απαρατήρητο.
Η εξίσωση

έχει λύση εκεί που τα διαγράμματα των

και

έχουν κοινά σημεία.
Τα κοινά αυτά σημεία μπορεί να είναι επί της πρώτης διχοτόμου

ή εκτός αυτής. Στην περίπτωσή μας όπως θα δούμε υπάρχουν μόνο τα πρώτα.
Τα επί της

δίνονται από τις λύσεις της εξισώσεως

λόγω συμμετρικότητας των διαγραμμάτων των

και

.
Έχουμε

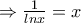

. Θα δείξουμε ότι αυτή έχει μοναδική λύση. Θεωρούμε προς τούτο τη συνάρτηση

η οποία στο διάστημα
![\left [ 1,e \right ] \left [ 1,e \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/ee7962eb8393aea22d8c5a1fe94157da.png)
πληροί τις προϋποθέσεις του Θ Bolzano άρα κάπου μεταξύ 1 και e, ας πούμε στο

, μηδενίζεται. Άρα έχουμε μια λύση

για την

ήτοι

(1)
Αν η συνάρτηση

μηδενιζόταν και σε άλλο σημείο έστω

τότε στο διάστημα των σημείων

και

θα πληρούσε τις προϋποθέσεις του Θ Rolle οπότε η παράγωγός της θα μηδενιζόταν κάπου μεταξύ των

και

. Όμως είναι

άτοπο διότι είμαστε εκτός ΠΟ.
Άρα επί της

έχουμε ακριβώς ένα κοινό σημείο.
Μια προτασούλα απαραίτητη πριν προχωρήσουμε:
Τα εκτός

κοινά σημεία των

και

εμφανίζονται κατά ζεύγη υπό την έννοια ότι όταν ένα σημείο είναι κοινό τότε είναι κοινό και το συμμετρικό του ως προς

.
Πράγματι επειδή τα διαγράμματα των

και

είναι συμμετρικά, αν

ένα σημείο και

το συμμετρικό του (πάντα ως προς

) έχουμε:

ανήκει στο διάγραμμα της

τότε

ανήκει στο διάγραμμα της


ανήκει στο διάγραμμα της

τότε

ανήκει στο διάγραμμα της

. Άρα

κοινό.
Αν τώρα τo

είναι ένα κοινό σημείο των

και

που δεν ανήκει στην

θα είναι:
α)

β) Το συμμετρικό του που είναι το

θα ανήκει επίσης στην

δηλαδή θα είναι

.
Αν η εξίσωση αυτή του β) υπό τη προϋπόθεση α) έχει λύσεις τη βάψαμε όλοι κατασκευαστής και λύτες. Όμως δεν έχει όπως αμέσως θα δούμε:
Όπως συνήθως θεωρούμε τη συνάρτηση

η οποία μηδενίζεται, όπως αμέσως θα δούμε, στο

που βρήκαμε πιο πάνω στο (1) (το οποίο βέβαια δεν πληροί την α) .
Πράγματι:

.
Αν η

μηδενιζόταν και σε κάποιο άλλο σημείο

τότε στο διάστημα των

και

θα πληρούσε τις προϋποθέσεις του ΘRolle οπότε η παράγωγός της θα μηδενιζόταν κάπου μεταξύ των

και

. Όμως

που δεν έχει λύση.
Άρα έχουμε μοναδική λύση για την

.
ΠΚ

 και
και 


 η εξίσωση
η εξίσωση  έχει μοναδική ρίζα.
έχει μοναδική ρίζα.

 και
και 


 η εξίσωση
η εξίσωση  έχει μοναδική ρίζα.
έχει μοναδική ρίζα.

 για κάθε
για κάθε  . Άρα η
. Άρα η  αφού
αφού  . Επίσης ο άξονας
. Επίσης ο άξονας  είναι οριζόντια ασύμτωτη της
είναι οριζόντια ασύμτωτη της 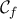 αφού
αφού  .
. 
 . Για την εύρεση αυτής έχουμε:
. Για την εύρεση αυτής έχουμε:
 οπότε εφαρμόζουμε DLH και έχουμε:
οπότε εφαρμόζουμε DLH και έχουμε:

 είναι σημεία της πρώτης διχοτόμου οπότε δίνονται από την
είναι σημεία της πρώτης διχοτόμου οπότε δίνονται από την 
 . Αν η
. Αν η  έπαιρνε την τιμή 1 περισσότερες φορές η παράγωγός της lnx+1 θα μηδενιζόταν εκτός πεδίου ορισμού. Το ότι η xlnx=1 έχει μια λύση προκύπτει από Bolzano στο [1,e].
έπαιρνε την τιμή 1 περισσότερες φορές η παράγωγός της lnx+1 θα μηδενιζόταν εκτός πεδίου ορισμού. Το ότι η xlnx=1 έχει μια λύση προκύπτει από Bolzano στο [1,e]. .
. στο
στο  .
.
 με παράγωγο:
με παράγωγο:



 και
και 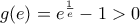




 από DLH.
από DLH.
 και όχι μηδεν
και όχι μηδεν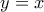 . Αυτό επικυρώνει την ορθότητα της (συμπυκνωμένης) αποδείξεώς μου για το 5. Θα το δείξω λίγο πιο κάτω.
. Αυτό επικυρώνει την ορθότητα της (συμπυκνωμένης) αποδείξεώς μου για το 5. Θα το δείξω λίγο πιο κάτω. ένα τέτοιο κοινό τους σημείο και
ένα τέτοιο κοινό τους σημείο και  το συμμετρικό του. Επειδή το
το συμμετρικό του. Επειδή το  είναι κοινό των συγκεκριμένων συναρτήσεων
είναι κοινό των συγκεκριμένων συναρτήσεων 
 θα είναι σημείο της
θα είναι σημείο της  . Στην προηγούμενη αναφορά μου είδαμε ότι η σχέση
. Στην προηγούμενη αναφορά μου είδαμε ότι η σχέση  που έχει μοναδική λύση έστω τη
που έχει μοναδική λύση έστω τη  . Αυτή είναι λύση και της
. Αυτή είναι λύση και της  Πράγματι είναι
Πράγματι είναι  . Αν υπήρχε και άλλη λύση σύμφωνα με το θ Rolle θα έπρεπε και η παράγωγός της δηλαδή η
. Αν υπήρχε και άλλη λύση σύμφωνα με το θ Rolle θα έπρεπε και η παράγωγός της δηλαδή η  να έχει λύση πράγμα αδύνατον καθ όσον
να έχει λύση πράγμα αδύνατον καθ όσον 
 μας δίνει τα επί της
μας δίνει τα επί της  πληροί τις προϋποθέσεις Bolzano στο διάστημα
πληροί τις προϋποθέσεις Bolzano στο διάστημα ![\left [ 1,e \right] \left [ 1,e \right]](/forum/ext/geomar/texintegr/latexrender/pictures/fb72a172f27a2245ea5d1e1303f36a43.png) δηλαδή
δηλαδή  Η λύση αυτή από την εν λόγω εξίσωση είναι μοναδική διότι: Αν υπήρχε και άλλη μία έστω
Η λύση αυτή από την εν λόγω εξίσωση είναι μοναδική διότι: Αν υπήρχε και άλλη μία έστω  τότε η συνάρτηση
τότε η συνάρτηση  που μηδενίζεται στο
που μηδενίζεται στο  που είναι εκτός πεδίου ορισμού.
που είναι εκτός πεδίου ορισμού. μηδενίζεται στο
μηδενίζεται στο  τότε στο διάστημα των
τότε στο διάστημα των  θα πληρούσε τις προϋποθέσεις Rolle οπότε η παράγωγός της θα έπρεπε κάπου εσωτερικά ατού του διαστήματος να μηδενίζεται. Η παράγωγος όμως είναι η
θα πληρούσε τις προϋποθέσεις Rolle οπότε η παράγωγός της θα έπρεπε κάπου εσωτερικά ατού του διαστήματος να μηδενίζεται. Η παράγωγος όμως είναι η  που μηδενίζεται αν
που μηδενίζεται αν 
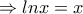 Όμως τέτοια σημεία δεν υπάρχουν διότι
Όμως τέτοια σημεία δεν υπάρχουν διότι 

 και
και 








 λόγω συμμετρικότητας των διαγραμμάτων των
λόγω συμμετρικότητας των διαγραμμάτων των 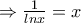
 . Θα δείξουμε ότι αυτή έχει μοναδική λύση. Θεωρούμε προς τούτο τη συνάρτηση
. Θα δείξουμε ότι αυτή έχει μοναδική λύση. Θεωρούμε προς τούτο τη συνάρτηση  η οποία στο διάστημα
η οποία στο διάστημα ![\left [ 1,e \right ] \left [ 1,e \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/ee7962eb8393aea22d8c5a1fe94157da.png) πληροί τις προϋποθέσεις του Θ Bolzano άρα κάπου μεταξύ 1 και e, ας πούμε στο
πληροί τις προϋποθέσεις του Θ Bolzano άρα κάπου μεταξύ 1 και e, ας πούμε στο  (1)
(1) άτοπο διότι είμαστε εκτός ΠΟ.
άτοπο διότι είμαστε εκτός ΠΟ.
 .
.  η οποία μηδενίζεται, όπως αμέσως θα δούμε, στο
η οποία μηδενίζεται, όπως αμέσως θα δούμε, στο  .
. μηδενιζόταν και σε κάποιο άλλο σημείο
μηδενιζόταν και σε κάποιο άλλο σημείο  που δεν έχει λύση.
που δεν έχει λύση.